Note: I'm using MathJax to code the mathematics in this webpage.
LaTeX macros are used to create commands out of bits of TeX/LaTeX code, usually for the purposes of
- making a short-hand version of something long,
- creating a command that can take parameters,
- creating a command that will change its effect depending on the environment it's in.
I want to say right now that I will not go over making macros to this third purpose because it's more difficult programming-wise than what I want to cover, and it's really beyond the scope of this introduction to LaTeX, and, lastly, because I'm not very good at it. However, I do want to highlight at least one example, and that is of the command
\frac{}{},
which comes standard in LaTeX. This command is used to typeset fractions of the form that use a horizontal bar to distinguish the numerator from the denominator. So, if we take as an example x = \frac{a}{b}, we get inline: x=\frac{a}{b}, and in the form within a displayed equation, we get x=\frac{a}{b}
The point is that the inline version is vertically compressed compared to the displayed math version, which means that the macro knows which math environment it's in and renders accordingly. By the way, one can still use the forms like a/b (the slant bar '/' being called by some the 'solidus') and a\div b. Note that the character '\div' is not on your standard keyboard, so you'll find it among the universe of special mathematical characters that can be looked up online, though you may need to declare some user package to get it to work. In this case, we can use the macro '\div' which is available in standard LaTeX.
One of many online sources of these lists of macros for special math characters (which include languages, dingbats, etc) is
https://www.caam.rice.edu/~heinken/latex/symbols.pdf
Basically, a macro is any command that begins with a '\', such as '\documentclass{article}'. But my interest in this article is in those macros that are defined either in the user packages, such as (to name two out of dozens!)
\usepackage{amsmath}
\usepackage{amssymb}
or those defined by the 'user' -- that's you or me, and we'll see plenty of examples of those coming up. By the way, feel free to barrow my macros all you want.
Typically, user-defined macros are placed in the preamble, but I have placed them just before the place that I need them in the code for ease of manipulating/editing while I'm putting them into their final forms, at which time I usually transfer them to the preamble.
There are a number of ways to create macros, but I'm only going to present two of them:
The older way is to use the
'\def' command,and the newer way is to use
'\newcommand' command.
The former goes back to Plain TeX (though you can still use them), and that is why my TeX files still have so many of them in the preamble -- I have been too lazy to convert them all, but I'm slowly getting around to it. The latter is available in LaTeX and has the advantage that it won't allow you to 'define' (or rather redefine) a command that has already been defined. You might be surprised how easy that is to do.
So, using the Plain TeX way to make macros, my first example is
\def\no{\noindent}In certain cases, I don't like the default indentation rules of LaTeX. The standard command '\noindent' turns off indentation for the immediate text line. The effect of the command '\no' is exactly that of '\noindent', but it's shorter, and to me, less intrusive looking.
The basic structure of the \def command is
\def\macro_name{TeX code}The TeX code inside the curly braces can pretty much be anything, even previously defined macros. The curly braces themselves are not part of the TeX code, so if you want to define a special environment, say for using a different font, then place your TeX code in between another pair of curly braces.
I often use boldfaced text characters to represent vectors in my mathematics. We can write macros for a few of them as examples:
\def\f{{\bf f}}The command '\bf' works within a text environment, and will cast the text in boldface font. This is standard in LaTeX. This environment is typically opened and closed by curly braces '{..}'.
\def\i{{\bf i}}
\def\j{{\bf j}}
\def\k{{\bf k}}
However, I don't tend to use single-letters macro names, anymore, so I would prefer these days to write these as
\def\boldf{{\bf f}}(I wouldn't write '\def\bf{{\bf f}}' because it's both confusing and circular.)
\def\bi{{\bf i}}
\def\bj{{\bf j}}
\def\bk{{\bf k}}
The macro
\def\calL{{\cal L}}allows us to use a caligraphic L as, \calL = \phi^\alpha\phi_\alpha + A, by using the code
\calL = \phi^\alpha\phi_\alpha + A,
Let's return to the \frac{}{} command. I used it three times inline to get the following rendering graphic:

The next graphic shows the code I used:

Now, to me, the first line doesn't look so good for the fraction. The default math environment between two single dollar signs is textsyle math. This fraction looks to me too compressed, so I fix it by forcing the math mode to be displaystyle by inserting between the dollar signs the command '\displaystyle'. And that takes care of the second line of the coding. For the third line, which is how I would really encode the math, uses the macro I defined
\def\dis{\displaystyle}
The point here is that the command '\dis' is less obtrusive to me than '\displaystyle', which is why I use it.
Say you want to use the symbol \widetilde v (encoded by '\widetilde v') in eight places in your large and complicated displayed equation. Complicated equations can cause both parentheses errors and the inability to know exactly where you are in the equation if debugging it. You could have fractions within fractions and square roots in fractions and it can get real complicated.
One way to remove some of the complication is to create a macro to replace a bunch of code. So, instead of using eight instances of '\widetilde v', instead define the macro
\def\tv{{\widetilde v}}and use eight instances of just '\tv'.
How about another example? In one of my papers I needed to produce the following n\times m matrix in multiple places:
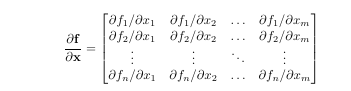
The code for this equation is
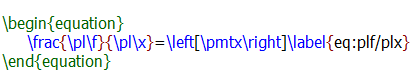
where the macro '\pl' was defined by me as
\def\pl{\partial}
The command '\left[..\right]' will place what's between them in an autoscaled pair of square brackets, as shown. The rows and columns were provided by the macro

It's a lot easier to use the macro '\pmtx' in an equation than to keep using the full code multiple times

If you're going to work with vectors, sometimes you have to place things over them. Here's a few examples:
\def\dotboldr{\dot{\bf r}}
produces \dotboldr.
\def\ddotboldr{\ddot{\bf r}}
produces \ddotboldr.
\def\boldhatv{\hat {\bf v}}
produces \boldhatv.
\def\hatA{\widehat A}
produces \hatA. Notice that you can use either \hat or \widehat, whichever you prefer.
From here on we'll use the \newcommand to define macros. The basic structure of this command is
\newcommand{\macro_name}{TeX stuff}
To invent our \noindent command, as before, but using the \newcommand instead is easy. The following command will work.
\newcommand{\no}{\noindent}
The following are a few macros I use frequently, but I'll let the reader figure them out.
\newcommand{\objective}{o\kern-.15pt{}b\kern-.3pt{}jective}
\newcommand{\sectionskip}{\vskip.2in}
\newcommand{\definedas}{\equiv}
\newcommand{\half}{\frac{1}{2}}
How do you put greek letters into bold font? Actually, there are a few ways to do this. One way is by use of the \boldsymbol command. The command
\newcommand{\bsigma}{\boldsymbol \sigma}
produces \bsigma in contrast to \sigma.
Now, let's create a macro that takes an argument. The command
\newcommand{\abs}[1]{\left|\,#1\,\right|}
and the equation
P^2 = \abs{x_1^2-x_2^2}
will produce the output P^2 = \abs{x_1^2-x_2^2} Now let's take the absolute value of something that will demonstrate how the autofit of the \left|...\right| operators work.
The equation
Q = \half\abs{\frac{x_1^2-x_2^2}{\sqrt{x_1^2+x_2^2}}} = \half\frac{\abs{x_1^2-x_2^2}}{\sqrt{x_1^2+x_2^2}}
will produce the output Q = \half\abs{\frac{x_1^2-x_2^2}{\sqrt{x_1^2+x_2^2}}} = \half\frac{\abs{x_1^2-x_2^2}}{\sqrt{x_1^2+x_2^2}}.
The structure of a macro that takes an argument is
\newcommand{\macro_name}[#args]{TeX code (with args)}
where #args is a value from 1 to 9.
Now, let's create an example macro that takes two arguments. The command
\newcommand{\fractoid}[2]{\half\frac{|\,#1\,|}{#2}}
and the TeX equation (in display mode)
Q = \fractoid{x_1^2-x_2^2}{\sqrt{x_1^2+x_2^2}}
will produce the output Q = \fractoid{x_1^2-x_2^2}{\sqrt{x_1^2+x_2^2}}
The macro \fractoid was expecting two user-supplied arguments to glom onto, so if the user doesn't provide them, an error message will be generated.
Sometimes you can look through a bunch of LaTeX math symbol lists for the right symbol but not find it. But maybe you can make it yourself. The command
\newcommand{\Rectangle}{\sqsubset\!\sqsupset}
and the equation
\Rectangle\ \not=\ \square
will produce the output \Rectangle\ \not=\ \square The command \sqsubset produces \sqsubset, and the command \sqsubset produces \sqsupset. So, I just mash them together, with the command '\!' in between them to remove a bit of space, and presto! Access these two symbols from the \usepackage{amssymb} package.