
The code to this is:

The code to this is:
The unipodal means to dealing with the Chebyshev Polynomials begins with the simple unipodal algebraic equation
\begin{equation}
X^{n}=b^{(n)}\,,\label{eq:TheFundamentalEquation}
\end{equation}
where $X=X_0+X_1u$ and $b^{(n)}=b_0+b_1u$, where $X_0,X_1,b_0,b_1$ are generally complex numbers and
$u^2=1$. We demand that
One difference between in-line and displayed math is that the latter tends to be rendered a bit larger than the former. In both modes, you can add a bit more space with the string '\,'. The default spacing in LaTeX is good, but not perfect, so I like to tweak it. By the way, to remove a little space, you can use '\!'.
Notice that LaTeX automatically placed an equation number to the displayed equation. That wasn't because I used a '\label' marker, for it would have anyway. You can tell LaTeX not to place an equation number by using the '\notag' marker, but some people, me included, think that LaTeX got this right. The idea is that every displayed equation should be numbered for ease of reference. Even if the author doesn't want to reference the equation later, the readers or reviewers of the article or book may. It can be very inconvenient to reference a displayed equation that is not numbered. By the way, another way to supress printing an equation number is to use the display command bookends
\begin{equation*}
.....
.....
\end{equation*}
As for the '\label' marker, I can reference the equation later by the command '(\ref{eq:TheFundamentalEquation})'.
Subscripts and superscripts are easy: Just use '_' for the former and '^' for the latter. By default, only the character immediately following one of these characters will be affected. The string 'X^{n}' is the same as the string 'X^n', but the string 'X^10' will not print the tenth power of X, but instead will print X10. For the tenth power, write 'X^{10}' to get X10.
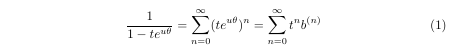
The code to this is:
\begin{equation}
\frac{1}{1-te^{u\theta}} = \sum _{n=0}^\infty (te^{u\theta})^n
= \sum _{n=0}^\infty t^nb^{(n)} \label{eq:Identity.over.unipodal.no.1st}
\end{equation}
As you can see, LaTeX is very tolerant of the use of spaces in the math code. You can even use hard returns --- just so long as you don't have a blank line in the math, and LaTeX will probably get it right.
LaTeX does the summation symbol well. It gets rendered a bit smaller in-line compared to displayed, which makes sense. But you can force LaTeX to print in displaystyle with the command '\displaystyle'. I use this command so frequently (especially within fractions) that I made a shorthand version of it
\newcommand{\dis}{\displaystyle}
Anyway, more about this kind of tweaking later.
Next,
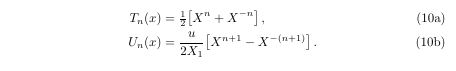
The code to this is:
\begin{subequations}
\begin{align}
T_{n}(x) &=\half\big[X^n+X^{-n}\big]\,,\label{eq:Chebyshev1st.Explicit.Unipodal}\\
U_{n}(x) &=\frac{u}{2X_1}\big[X^{n+1} -X^{-(n+1)}\big]\,.\label{eq:Chebyshev2nd.Explicit.Unipodal}
\end{align}
\end{subequations}
There's a lot to unpack here. Let's start with fractions. Of course you can do fractions in a line with, say, 'a/b'. And that manner of dong it may be preferred in exponents. But you can also do vertical fractions using the command '\frac{a}{b}'. Sometimes the result for a trivial fraction like '\frac{1}{2}' in display mode looks too large in some contexts -- at least to me. My fix to this was to invent the macro for 1/2 as shown below.
\newcommand{\half}{{\textstyle{1\over 2}}}I have made many others, as well. That command '\textstyle{}' forces the smaller textstyle rendering, but only within the curly braces.
\newcommand{\third}{{\textstyle{1\over3}}}
\newcommand{\fourth}{{\textstyle{1\over 4}}}
If I had left the sizing of the square brackets to LaTeX, it would have endered them a little smaller. This doesn't seem to bother most people, but I prefer them a bit larger. And that's where the commands '\big[' and '\big]' came in. LaTeX let's us use an assortment of resizing commands in the same stripe: '\Big[', '\bigg[', '\Bigg['. This command works for the various delimiters. But if you want a big curly brace, remember to escape it first: '\Big\{'. LaTeX also does automatic resizing with the '\left(' and '\right)' commands. But remember that the compiler expects to see both of these if it find one. If you only use one of the autoresizing commands, you'll get an error message. However, you do not have to follow a '\Big[' with a '\Big]'. If you only want the left [, say, autoresized (but you don't have a right ]), you can do this with first a '\left[', follwed by a '\right.'.
Now, for aligning equations.
\begin{align}Typically, one will align on the equation's equal signs, and that's where the ampersand & comes into play. In another section, we'll go over more difficult equation alignment situations.
T_{n}(x) &=\half\big[X^n+X^{-n}\big]\,,\label{eq:Chebyshev1st.Explicit.Unipodal}\\
U_{n}(x) &=\frac{u}{2X_1}\big[X^{n+1} -X^{-(n+1)}\big]\,.\label{eq:Chebyshev2nd.Explicit.Unipodal}
\end{align}
Before leaving this section, we look at the command for subequations, meaning the grouping of equation by the same equation number, but adding a letter after each one in advancing order. The command for this is the pair is
\begin{subequations}In between those bookends you can put not only multiple equations but also text.
.....
.....
\end{subequations}
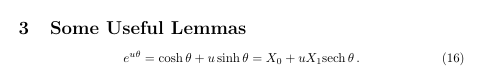
The code to this is:
\section{Some Useful Lemmas}(By the way, the displayed equation (16) is not correct; it was rewritten just for demonstration purposes.)\begin{equation}
e^{u\theta} = \cosh \theta + u \sinh \theta = X_0 + u X_1\sech\theta\,.
\end{equation}
In LaTeX, you can access greek letters easily (in math mode) by just spelling them out: \alpha, \beta, \gamma, etc. And their capitals: \Alpha, \Beta, \Gamma. Likewise, you can access common trigonometric functions: \cos, \sin, \tan. And hyperbolic trig functions: \cosh, \sinh, \tanh. But you may have trouble with \sech. Below, I offer a quick and dirty macro solution for it:
\newcommand{\sech}{\text{sech\,}}There's no time like the present to start writing your own simple macros.
Next,
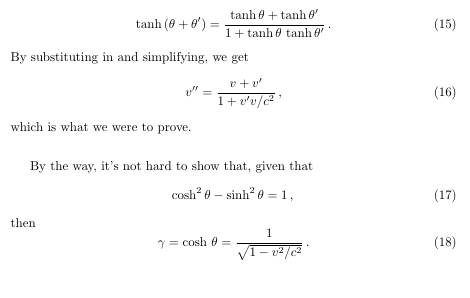
The code to this is:
\begin{equation}That command '\substituting\ ' uses my macro
\tanh\,(\theta+\theta') = \frac{\tanh\theta + \tanh\theta'}{1+\tanh\theta\,\tanh\theta'}\,.\label{eq:tanh=}
\end{equation}
By \substituting\ in and simplifying, we get
\begin{equation}
v'' = \frac{v+v'}{1+v'v/c^2}\,,\label{eq:SRformula2nd}
\end{equation}
which is what we were to prove.
\vskip.25in
By the way, it's not hard to show that, given that
\begin{equation}
\cosh^2\theta - \sinh^2\theta = 1\,,\label{eq:Identity=}
\end{equation}
then
\begin{equation}
\gamma = \cosh\,\theta = \frac{1}{\sqrt{1-v^2/c^2}}\,.\label{eq:gamma=}
\end{equation}
\newcommand{\substituting}{su\kern-.3pt{}b{}stituting}to close up the letter spacing a bit in the word 'substituting' compared to how LaTeX would render it. The '\ ' at the end makes sure that a space is inserted between the macro-defined word and the following word. If, however, you are going to end the macro '\substituting' with some punctuation, then no backslash is needed. For example, '\substituting,' will work just fine.
The squareroot command is new to this presentation. Remember that in most cases the sqrt(1-v2/c2) can be also rendered as (1-v2/c2)1/2. So, choose the one that you think looks the better, if that choice is left to you.
And while we're on the topic of the square root symbol, compare the following renderings:
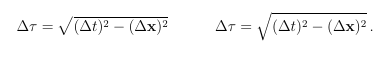
So, we are back to the art of subtle spacing. To me, the squareroot on the left looks a bit vertically cramped. To add some vertical space under the squareroot sign, I added the command '\strut' somewhere inside the command \sqrt{}. The comparison follows:
\Delta \tau = \sqrt{ (\Delta t)^2 - (\Delta \bx)^2} \hskip.5in \Delta \tau = \sqrt{\strut (\Delta t)^2 - (\Delta \bx)^2}
The \strut is a vertical rule of zero thickness (see the \rule command). You can define your own struts (of various heights) by use of the \rule command.
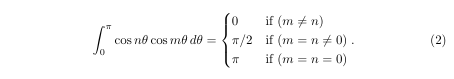
The code to this is:
\begin{equation}The big curly brace is part of the LaTeX command
\int_{0}^{\pi}\cos n\theta \cos m\theta\, d\theta
= \begin{cases} 0 &\mbox{if } (m\ne n) \\
\pi/2 &\mbox{if } (m= n \ne 0) \\
\pi & \mbox{if } (m= n = 0) \end{cases}.\label{eq:MainIntegralTrigForm}
\end{equation}
\begin{cases} ... \end{cases}The integral sign will be rendered differently in textstyle mode vs displaystyle mode. I ussally force LaTeX to use the displaystyle of the integral in text, even though it creates a little extra separation of the lines of text.
Note that the cases render three rows. The first two rows are terminated by '\\'. I'll leave it to the reader to look up the command elsewhere for details. But I have two points of interest to make at this time. First, the use of the & symbol on each line creates a line of vertical alignment. Second, '\mbox{if }' creates a non-math mode (or text mode) for rendering, hence the 'if ' is printed in regular text, not math italic.
Normally, LaTeX does a great job on its own to make to right choice of size of superscripts and subscripts when all the symbols of in math italic. But what is you want some subscript, say, to be in textfont (whatever you are using or desire)? The solution for this is simple: Just place the subscript inside of an \mbox{}. That will get the font right, but maybe not get the size right.
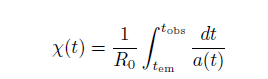
Notice that the subscripts on t are in textfont, not in math-italic font. The code I used for this is
![]()
Some of the pre-defined commands one can choose form to adjust the size of text are
\tiny, \scriptsize, \footnotesize,
\small, \normalsize, \large,
\Large, \LARGE, \huge, \Huge.
How do you deal with an overly long equation? The following is such an equation.
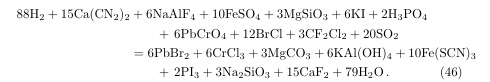
And then my encoding of it. (Notice that overly long equations can run passed the right margin.)

And that's all for this chapter.