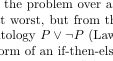
The code for the math/logic part is:
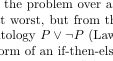
The code for the math/logic part is:
$P\vee \neg P$
You can do an Internet search for more logic symbols. One site I found is
https://www.geeksforgeeks.org/logic-notations-in-latex/
Next, the following figure shows a matrix being operated on by a function, yielding
another matrix.
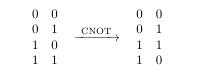
To get the matrix, use the command \begin{matrix}...\end{matrix}. The long right-pointing
arrow (of variable length) is special, in that it's not in the list of LaTeX math symbols.
It's made with the command [required: \usepackage{amsmath} ]
\xrightarrow{\text{ CNOT }}You can place whatever symbols you want in the textbox (within reason) and the length of the
Next, for those who typeset some quantum mechanics, I give my definitions of bra, ket, and braket:
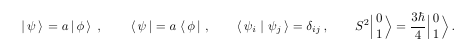
The following code has the definitions I made for these objects:
\def\ket#1{\left|\,#1\,\rangle\right.}
\def\bra#1{\left.\langle \,#1\, \right|}
\def\braket#1#2{\left\langle \,#1\left. \right|\,#2 \,\right\rangle}
\def\bigket#1{\Big|\,#1\,\Big\rangle}
The following code shows how I used these definitions in the above figure:
\begin{equation}
\ket{\psi} = a\ket{\phi}\,,\qquad \bra{\psi} = a\bra{\phi}\,,\qquad \braket{\psi_i}{\psi_j}
= \delta_{ij}\,,\qquad S^2\bigket{\begin{matrix} 0\\ 1 \end{matrix}} =
\frac{3\hbar}{4}\bigket{\begin{matrix} 0\\ 1 \end{matrix}}
\,.
\end{equation}
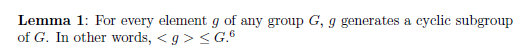
\begin{equation}
\no {\bf Lemma 1}: For every element $g$ of any group $G$, $g$ generates
a cyclic subgroup of $G$. In other words, $< g >\ \le G$.\footnote{This lemma
is true whether $G$ is finite or infinite.}
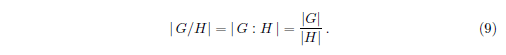
\begin{equation}
|\,G/H| = |\,G:H\,| = \frac{|G|}{|H|} \,.\label{eq: |G/H|}
\end{equation}
The '\,' commands add a little bit of space, which I have use here for purely aesthetic purpuses.
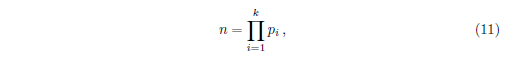
\begin{equation}
n = \prod_{i=1}^k p_i \,,\label{eq:FTofArithmetic}
\end{equation}
The reader should remember that there's often a big difference in how math is rendered in-line vs in a displayed equation, such as the above.
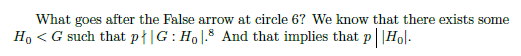
What goes after the False arrow at circle 6? We know that there exists some
$H_0 < G$ such that $p\nmid |\,G:H_0\,|$.\footnote{That's one of the
advantages of using a `for all' -- its negation implies that `there exists'
something, and that could be useful.} And that implies that $p\,\,\divides\, |H_0|$.
Some commands, like \nmid, may required you to use special packages, like 'amssymb' [\usepackage{amssymb}].
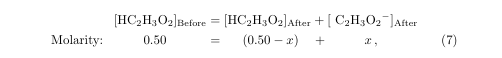
The code to this is:
\begin{align}
[\text{HC$_2$H$_3$O$_2$}]_\text{Before} &= [\text{HC$_2$H$_3$O$_2$}]_\text{After} + [\text{ C$_2$H$_3$O$_2{}^-$}]_\text{After}\notag\\
\text{Molarity:} \hskip.43in 0.50\hskip.43in &= \hskip.2in (0.50-x)\hskip.142in +\hskip.15in\hskip.243in x\,, \label{eq:acetatebeforeafter3.1}
\end{align}
There are a number of commands that one can use to insert regular text into a math environment. One of these is the \text{} command, but I have also used \hbox{} and \mbox{}. The '\notag' command prohibits the compiler from placing an equation number on that particular line.
Next,
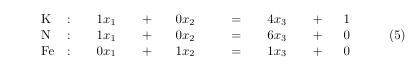
The code to this is:
\begin{equation}
\begin{array}{llllllllllllllllll}
&&\K&: &&1x_1 &&+ &\hskip8pt0x_2 &&\hskip8pt = &&4x_3 &&+ &&\hskip-4pt1\\
&&\N&: &&1x_1 &&+ &\hskip8pt0x_2 &&\hskip8pt = &&6x_3&&+ &&\hskip-4pt0\\
&&\Fe&: &&0x_1 &&+ &\hskip8pt1x_2 &&\hskip8pt = &&1x_3 &&+ &&\hskip-4pt0\label{eq:Array}
\end{array}
\end{equation}
I have created arrays in many different way in LaTeX over the decades, and I am no expert, but this is one way I did it. The '&' characters define tabs for vertical alignment. I'll go over arrays in a separate webpage.
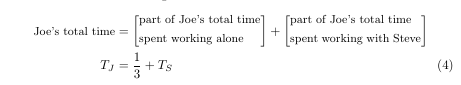
The code to this is:
\begin{align}
\text{\ninerm Joe's total time} &= \left[\raisebox{-.081in}{\vbox{\ninerm\hsize=1.3in\no part of Joe's total time\newline
spent working alone}}\right]+\left[\raisebox{-.081in}{\vbox{\ninerm\hsize=1.4in\no part of Joe's total time\newline
spent working with Steve}}\right]\notag\\
T_J &= \frac{1}{3} + T_S
\end{align}
LaTeX is really good at rendering pure mathematics, but it doesn't always look pretty to render text (especially in paragraph form) in a box mixed in with the mathematics, as I like to do. My solution, elegant or not, has been to create hboxes and vboxes to place text within. These primitive TeX commands go back to when I first start with TeX, which was with Plain TeX. I was even able to use the command 'newline' to force the text to start a new line within the vbox.
The command '\no' is my personal short for \noindent. The font command 'ninerm' defines roman type of size nine points [\font\ninerm=cmr9 ]. This looks better to me than the default ten-point type.
The command '\raisebox' raises or lowers a box that has something in it.
A tricky equation alignment. The following code produces the graphic output after it:
\begin{align}
y(x) &= \int_a^b \frac{f(\tau)\phi_1(\tau)\phi^1(x)}{W(\tau)}\,d\tau - \int_a^x \frac{f(\tau)\phi_\alpha(\tau)\phi^\alpha(x)}{W(\tau)}\,d\tau\notag\\
&= \int_a^x \frac{f(\tau)\phi_1(\tau)\phi^1(x)}{W(\tau)}\,d\tau +\int_x^b \frac{f(\tau)\phi_1(\tau)\phi^1(x)}{W(\tau)}\,d\tau\notag\\
&\quad-\int_a^x \frac{f(\tau)\phi_\alpha(\tau)\phi^\alpha(x)}{W(\tau)}\,d\tau\qquad\qquad\begin{array}{ll}\mbox{(\eightrm we broke up the 1st integral of the}\\
\mbox{\quad\eightrm previous line and we'll simplify by}\\ \mbox{\quad\eightrm combining the 1st and 3rd terms)} \end{array} \notag\\
&= - \int_a^x \frac{f(\tau)\phi_2(\tau)\phi^2(x)}{W(\tau)}\,d\tau +\int_x^b \frac{f(\tau)\phi_1(\tau)\phi^1(x)}{W(\tau)}\,d\tau\quad\begin{array}{ll}\mbox{(\eightrm now, we raise the}\\ \mbox{\eightrm \quad lower indices)}\end{array} \notag\\
&= \int_a^x \frac{f(\tau)\phi^1(\tau)\phi^2(x)}{W(\tau)}\,d\tau + \int_x^b \frac{f(\tau)\phi^2(\tau)\phi^1(x)}{W(\tau)}\,d\tau \,.\label{eq:GFDetermined}
\end{align}

I wanted to place comments on the line it was needed. To do this, I had to use a smaller font than 10 point. So, in the preamble is the font definition
\font\eightrm=cmr8