On this page, I present various proofs about cones and planes, using geometric algebra
as the main computational tool.
Download PDF file: Proof that a level plane intersects a vertical cone in a circle.
Download PDF file: Euclidean geometry and Geometric Algebra are used for the
following problem
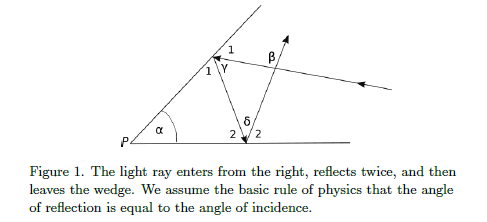
Figure 1 depicts a wedge that is reflective on its insides. A light ray enters it from
the right, reflects twice off the interior of the wedge and then exits, passing the
incoming path along the way. The angle of the wedge at $P$ is $\alpha$. The angle that
the incoming and outgoing rays make is $\beta$. Show that $\beta = 2\alpha$. We'll solve this
two ways: First, with Euclidean geometry and second with Geometric Algebra.
It is assumed that the reader already knows the basics of geometric algebra.