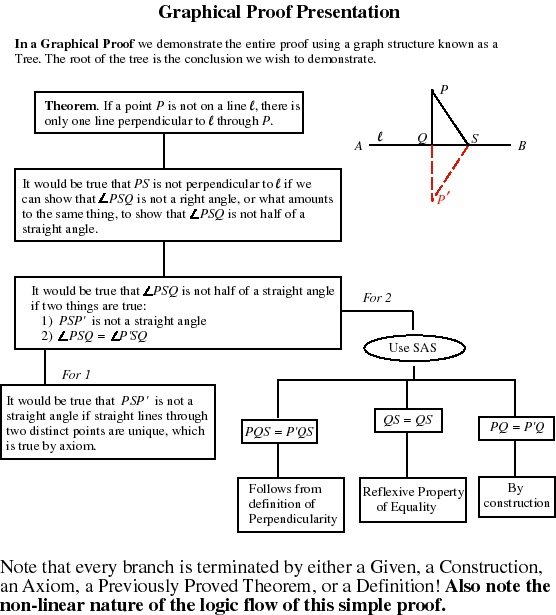
There is an area of mathematics known as graph theory which deals with the analysis and practical usage of graph structures, which can be described simply of vertices and edges. In the figure below the vertices are the rectangles and the edges are the line segments connecting them. The particular graph structure below is called a Tree. Specifically, a Tree is a connected graph that has no cycles. Most proof can be graphed as trees, but not all proof are without cycles. FOr example, suppose that a particular proof can use exhaustive search of some functional value over some finite integer index. Then a for-loop or a repeat-until loop might be appropriate.
The main purpose of the graphical representation is to further clarify the main logical connections of the proof, building on the connections revealed in the pseudo proof presentation. It also helps to reveal the heuristics used in discovering the proof. But more than any other function the graph has is to reveal the non-linearity of proofs. Note, however, that the logical tree of graph theory need not resemble any real tree.
The proof presented below is based on analysis presented in the previous page.
