Download PDF file: Determinant Form of the Area of a Triangle(by Geometric Algebra)
Problem: Show that the area of the triangle given in Fig. 1 has the determinant form (which I found in some textbook) \begin{equation} \text{Area} = \pm\frac{1}{2} \left| \begin{array}{ccc} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1\\ \end{array}\right|\,,\label{eq:Determinant} \end{equation} where the $\pm$ sign accounts for the two possible orientations of the bivector formed in the process. This formula is useful if one already has the coordinates of each of the three vertices.
Note: At the end of this article are some notes for those readers unfamiliar with geometric algebra.
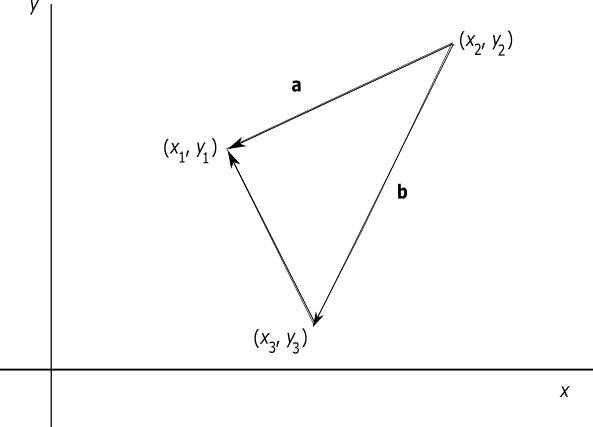
Figure 1. We have arbitrarily labeled one side as vector $\ba$ and another
as $\bb$. (We only need assign two sides with vectors.) The only difference
that will occur in the assignment of $\ba$ and $\bb$ will be an overall sign.
Actually, we are dealing here with two forms of area: a bivector form and a scalar form, such as in Eq. (\ref{eq:Determinant}). The bivector form of the area is given (nonuniquely) below \begin{equation} \text{Bivector Area}\ \triangle = \half\ba\wedge\bb\,,\label{eq:a_wedge_b} \end{equation} which, in this case, assigns a positive orientation to the bivector. To arrive at the scalar form of the area, let $\bsigma_1$ and $\bsigma_1$ be, unit vectors along the $x$- and $y$-axes, respectively. Then, \begin{equation} \text{Scalar Area}\ \triangle \definedas \half\ba\wedge\bb \cdot \bsigma_1\wedge \bsigma_2\,.\label{eq:a_wedge_b.s_1_wedge_s2} \end{equation} By convention, vectors $\ba$ and $\bb$ in coordinate form are given as \begin{align} \ba &= (x_1 - x_2,\, y_1-y_2)\,, \notag\\ \bb &= (x_3 - x_2,\, y_3-y_2)\,. \end{align} Therefore, \begin{align} \text{Scalar Area}\ \triangle &= \half\ba\wedge\bb \cdot \bsigma_1\wedge \bsigma_2 \notag\\ &= \half\ba\cdot [\bb \cdot \bsigma_1\wedge \bsigma_2 ] \notag\\ &= \half\ba\cdot [\bb \cdot \bsigma_1 \bsigma_2 - \bb \cdot \bsigma_2 \bsigma_1] \notag\\ &= \half[\ba\cdot \bsigma_2 \bb \cdot \bsigma_1 - \bb \cdot \bsigma_2 \ba\cdot\bsigma_1] \notag\\ &= \half[(y_1-y_2) (x_3-x_2) -(y_3-y_2) (x_1-x_2)]\,. \end{align} On expanding this one more step, we get the same result that we get by expanding (\ref{eq:Determinant}).
QED
By the way, if we had taken $ \half\bb\wedge\ba$ as the bivector area, we would have gotten the negative value of the above result, hence, the $\pm$ sign in Eq. (\ref{eq:Determinant}).
Point 1. The reader who is not familiar with geometric algebra and wedge products, can reference on-line sources through the search string `wedge product'. The main reference book is New Foundations for Classical Mechanics by David Hestenes (Kluwer Academic Publishers). An online reference is
Download PDF file: A Geometric Algebra Primer by David Hestenes
Point 2. The area of a triangle is typically computed by taking half the wedge product of any two sides.