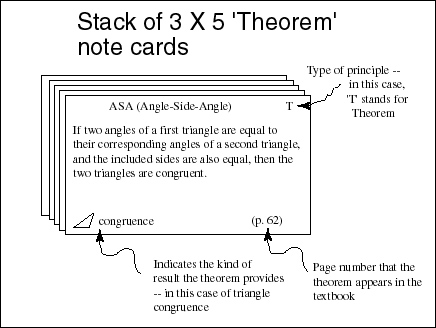
Fig. 1. The theorem stack of cards
Introduction:
I have long been an advocate of students memorizing the main theorems and definitions in a given math class, keeping up with the needs of the class. What I will exhibit the placing of a math demonstration/proof in a flow chart. This is particularly useful when one has to deal with parallel logic streams, but less useful with only one logic stream. What would one logic stream look like? Well, something like going from given A to result R:
I have written some other articles on doing geometry. First, one on using the patterns of similar triangles found in
Euclidean Geometry Problem Solving
Using the Wedge.
Preparation to solve a problem: Have your stack of geometry note cards with theorems and definitions.

Fig. 1. The theorem stack of cards
In Fig. 1 we see a representation of a particular theorem card. This stack of cards can also contain all lemmas (which are special theorems singled out by history or by a particular author, usually to be used within a proof of some important theorem to reduce the number of steps in the important theorem) and corollaries (which are theorems immediately deducible from some other theorem with some additional piece of information).
The theorem stack has at least five main pieces of information: The theorem name, the theorem statement, a card classification letter for easy collecting of cards into stacks, the page number that the theorem appears in the textbook, and a characterization of the kind of topic the theorem deals with. The principle is either a definition, a theorem, a postulate, or specific given information from the problem.
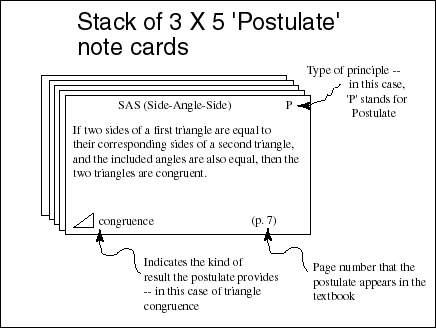
Fig. 2. The postulate stack of cards
Postulates are rules that are assumed to be true and are used to jumpstart the whole subject of geometry.
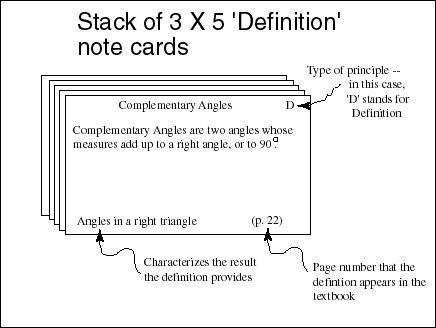
Fig. 3. The definition stack of cards
As we attempt to solve a problem backwards, we will diagram our progress by using a graph. A graph is a combination of nodes connected by straight or curvy lines. Our graphs will be in a special form, called a tree. A tree is a graph that has no cycles, that is, no loops in it, and we say that each branch of the tree is a leaf. Each leaf is some principle, i.e., a postulate, theorem, definition, or given information. One nice aspect of this method advocated here is that it directly facilitates the student to automatically use the heuristic of making sure to used all, or at least enough of, the given information to be able to finish the proof. An example of the building of a "proof tree" we will formulate in backward problem solving is given below:
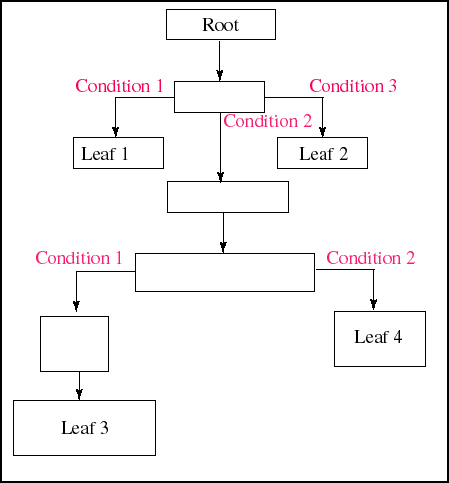
Fig. 4. A generic tree structure
I should point out that I have posted math proofs on this website that do use loops,
but I never found that necessary in high-school geometry problems.
Let's try out our technique on a real problem. Look at the figure below:
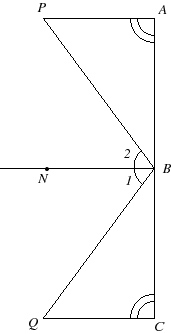
Fig. 5. Example problem.
Angle A is congruent to angle C, and angle 1 is congruent to angle 2. NB is perpendicular to AC at B. Show that triangle PBA is congruent to triangle QBC. (I'm not going to distinguish in this demonstration between angle congruence and equality.)
Using the backward problem-solving technique, we ask ourself: What is
one step away from concluding the proof? In other words, what statement,
if true, would immediately imply the theorem? So, you see that we KNOW
precisely where to start. We start with the conclusion and work backward.
How many times have I heard a student say that he or she doesn't even know
where to start the problem. Well, now we know the start. This is the first
rule of any heuristic set of problem solving techniques -- knowing where
to start. By the way, there may be more than one way to start this problem,
but any way the gets the right answer is fine.
GETTING GOING:
I said before that this method has a specific beginning, middle, and end, and this will be demonstrated in the proof below.
Proof:
THE BEGINNING
Given that triangle PBA can be put into correspondence with triangle
QBC,
with angle ![]() A corresponding
to
A corresponding
to ![]() C, angle
PBA corresponding to angle QBC, and side BA with side
BC, then it seems immediately clear to me that the two triangles
are congruent if we can prove, invoking the Angle-Side-Angle theorem,
that
C, angle
PBA corresponding to angle QBC, and side BA with side
BC, then it seems immediately clear to me that the two triangles
are congruent if we can prove, invoking the Angle-Side-Angle theorem,
that ![]() QBC =
QBC = ![]() PBA.
PBA.
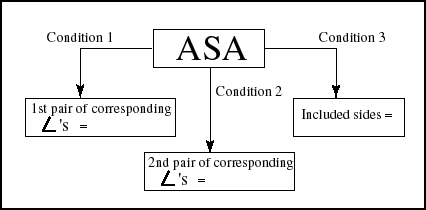
Fig. 6. Generic tree representation of the ASA theorem.
THE MIDDLE:
After getting an idea of some principle to use to support the "last"
step (i.e., the step just before the theorem is finished being proved),
we use the same process, repeatedly applied to each of its conditions,
and then we repeatedly perform the same kind of procedure for each condition
until the process ends by terminating each branch of the tree with some
principle which is true without comment. This last statement is ambiguous
and this cannot be helped, as it true that the problem solver has some
leeway to the amount of rigor the problem solver wants to use.
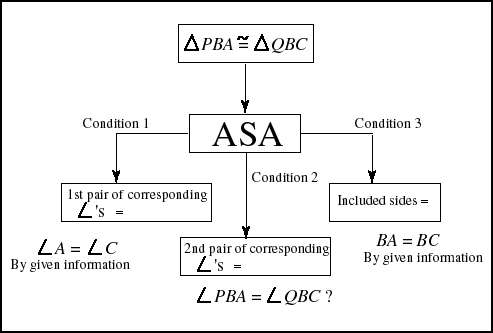
Fig. 7. The first principle used here is ASA theorem. It has
three conditions of its own to satisfy. In this problem the
given information is used a lot to terminate branches.
THE END:
We've arrived at the end because every branch has been terminated by a principle which needs no further justification, at least to the satisfaction of this problem solver.
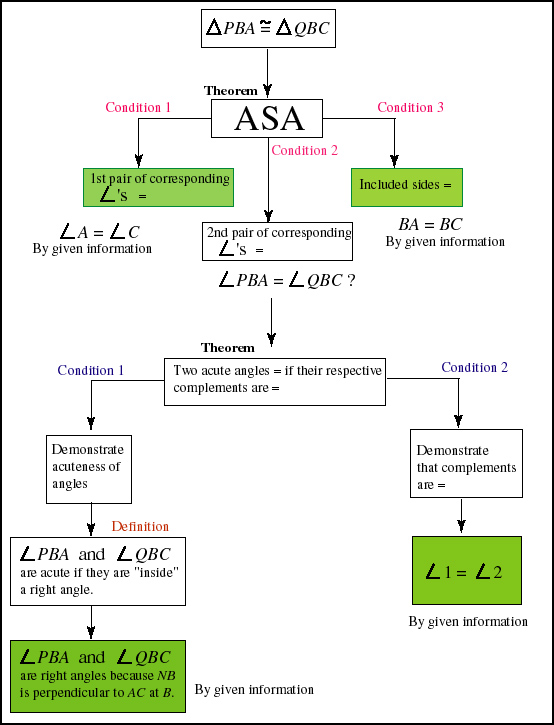
Fig. 8. The full tree has been formed. In this particular problem
has all the leaves as given information.
All that's left to do now is to put the proof together into a linear looking form, called a two-column proof:
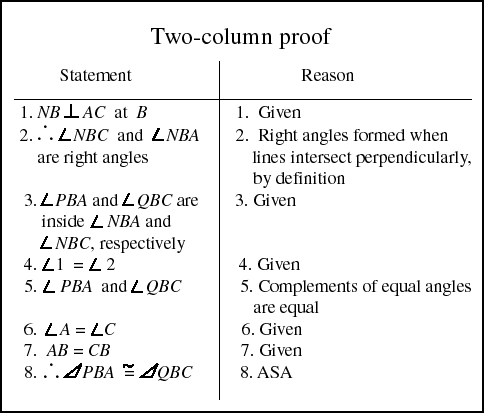
Fig. 9. The Two-Column form of proof.
Conclusion:
The Two-Column form of proof for our problem by itself makes it look
like the problem solver just starts at the top (who knows why though) and
linearly move step-by-step to the last step. The diagramming approach
reveals that many proofs are not linear.