More Wedge Stuff | Eucl Geom Found Alg | Solved problems using Wedge Geometry | The Wedge and Real Numbers

Euclidean Geometry Problem Solving

Semi-gratutitous cool figure showing multiplication! Note that the product of a with b is accomplished without recourse to digital computation. In terms of map phraseology: The map that takes the unity to b takes a to ba. A "map," as it is used in this sense, is signified by a letter with an underline.

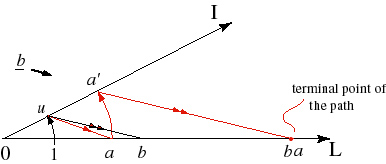
Wedge Technology is the name I gave to the use of similar triangles formed whenever two parallel lines in a plane cut a pair of intersecting lines all in the same plane. Much can be accomplished just by using "straight-edge and ruler" like constructions, such as the construction of the rational number system. Yet much more is accomplished by adding in iterative operations and successive refinement operations.

After I had developed the obvious applications of Wedge Technology to high school algebra, I came across David Hilbert's book, Foundations of Geometry (Second English translation, Open Court, La Salle, Ill., Ninth Printing 1997), which uses much the same approach to introduce the axioms of the real numbers. However, his treatment is considerably broader in scope and yet lacks the mapping perspective, the construction of inverses, recursive multiplication, and extraction of nth roots. Even so, it shows us ways to further develop Wedge Technology.

Click to download paper (first written in late 1997):

   Download Now | Euclidean Geometry Problem Solving Through Symmetry Analysis

This paper champions the cause of using the Wedge and other nonstandard geometric constructions to use in solving geometry problems. The best I can do here is to give a couple examples of how it works.

Example One

In the figure below AH = m1, HF = m2. The lines with arrows are mutually parallel to each other. The three triangles, AFG, ADE, and ABC, are isosceles. What is the length of line segment DB in terms of m1 and m2?

Solution to Example One

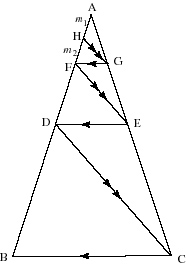
Obviously we have a definite Wedge and a definite linear map from AB to AC. Let's call our linear map M, which takes the point H to the point G.

Then, since AG = m1 + m2, M(m1) = m1 + m2, and Mn(x) = (m1 + m2)n x/m1n.

Example Two

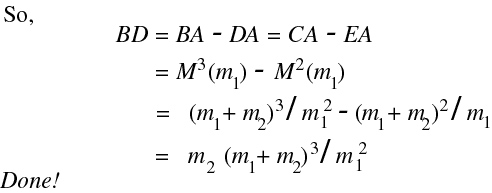
To accomplish this next example, we'll need the use of a theorem, which I refer to as the Circular Half-Angle Theorem or CHAT: The measure of an inscribed angle in a circle intercepting a minor arc is equal to half the measure of the central angle intercepting the same arc.

In the figure below we see that triangle ABC has a point D placed on it such that OVERLINE(AD) bisects angle A. Show that BD/DA = CB/CA.

Solution to Example Two

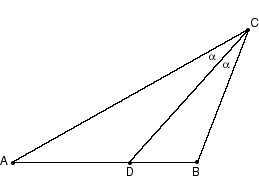
Since we are to prove a proportion, and since a proportion suggests a Wedge with parallel lines going through it, we will take point A as the vertex of our Wedge and device what the parallel lines are to be. For our solution here we'll take OVERLINE(CD) as one line and draw through B a line parallel to it.

However, our procedure will be somewhat indirect at this point. Let's make C the center of a circle of radius CB. Then extend OVERLINE(AC) to meet the circle at F. The figure is shown below.

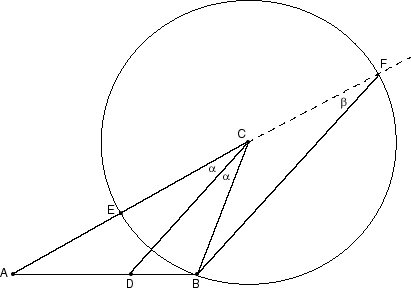
From the CHAT theorem we deduce that angle alpha = angle beta. So OVERLINE(CD) is parallel to OVERLINE(BF). From this we conclude that FC/CA = BD/DA. But FC = CB, so CB/CA = BD/DA, which is what we were to show.

   More Wedge Stuff | Wedge Technology