More Wedge Stuff | Wedge Technology Start Page

The Wedge and Real Numbers

Semi-gratutitous cool figure showing multiplication! Note that the product of a with b is accomplished without recourse to digital computation. In terms of map phraseology: The map that takes the unity to b takes a to ba.

The link below is a pdf file that more fully develops the use of Wedge Technology to lay a foundation to the real numbers. The paper is entitled "Euclidean Geometry as a Foundation to the Real Numbers." In it we develop the axioms of the reals in a geometric way that is very intuitive. Commutivity and assocoiativity of the reals are discussed, along with the extraction of n^th roots of positive reals by use of a RAM diagram! Also discussed are the construction of inverses of reals and the basic inequalities of algebra.

This paper is 100% Constructionist in its philosophy of education. First the student constructs the integers (enough to get the idea anyway) with straight edge and ruler, choosing an arbitrary unit at the start. Then he or she contructs the field of rationals using Wedge Technology. From that point special irrational reals can be added to the system by geometrical constructions.

This paper lays a foundation for the next in the series entitled "Euclidean Geometry Problem Solving Through Symmetry Analysis: Transformations and Embeddings," which has a link at the top of the page. It also uses the Wedge and other unusual devices in the usual synthetic approach to proofs in high school geometry.

Click to download paper (first written in late 1997, but recently updated, April 2020):

Download Now | Euclidean Geometry as a Foundation to the Real Numbers

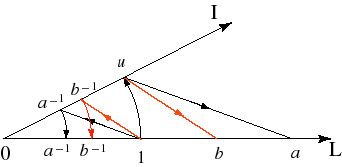
Let's go over a couple uses of the Wedge that are described in the above paper. First, given b < a, show that a^-1 < b^-1. The geometrical construction is given in the figure below.

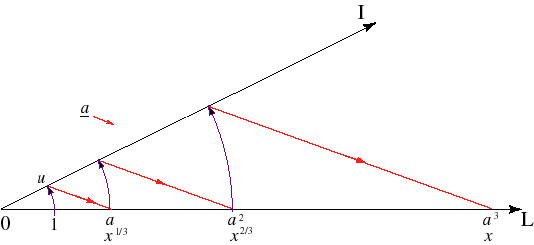
Next, find by construction the real number 5^2/3. To accomplish this we'll use the RAM diagram--RAM for Recursive Analog Multiplication.