Patrick Reany
Abstract: This page presents mathematics diversions, which are basically just
math problems of varying difficulty, which one can try to solve for fun or for
testing one's math skills, or for learning new methods and concepts.
Disclaimer: Many of the following problems were taken from SATs or old
Olympiad tests. My alternative solutions may not follow Olympiad rules, however.
The techniques I use may not be fit for use in Olympiads or entrance exams or the like.
I believe that it's good to see alternative solutions to better fill out one's
mathematical abililties. Four decades ago, I quipped that one cannot truly
understand a theorem until one is able to prove it in essentially two different ways.
It's meant to be a thought-provoking claim, perhaps containing a morsel of truth.
This problem (#1) is found on the YouTube channel PreMath, from
December 25, 2021.
One can find my solution to this problem at Solution to this problem.
This problem (#2) is found on the YouTube channel PreMath, from
December 23, 2021.
Statement of the problem:
One can find my solution to this problem at Solution to this problem.
This problem (#3) is found on the YouTube channel Math Window, from
September 7, 2022.
Statement of the problem: Find a solution for a,b,c given the
the system of equations as follows:
The presenter's solution is perfectly good, and perhaps the shortest. However, my solution
This problem (#4) is found on the YouTube channel MindYourDecisions, from
July 5, 2015. My solution here is a little different from that
given by the presenter:
My solution is found here Solution to this problem.
This problem (#5) is found in my sixth Ilfinor fiction novel.
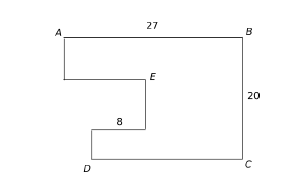
Statement of the problem: Find the perimeter of the following figure.
My solution is found here Solution to this problem.
This problem (#6) is found on the YouTube channel Ankit Math Magics, from
April 14, 2023:
My solution to the problem Solution to this problem.
This next problem (#7) is found on the YouTube channel MindYourDecisions, from
14 September, 2023: "People are arguing about a simple geometry problem. Can you solve it?"
My solution to the problem Solution to this problem.
This next problem (#8) is found on the YouTube channel Logically Yours, from
30 January 2021:
My solution to the problem Solution to this problem.
This next problem (#9) is found on the YouTube channel
Statement of the problem:
If the angle bisectors of two vertices of a triangle are congruent, show that the triangle is isosceles.
This is a well-known problem in the literature, and not without some considerable controversy,
My solution to the problem is pending. I tried it, but haven't succeeded yet.
This next problem (#10) is found on the YouTube channel Prime Newtons, titled "1995 British Mathematics Olympiad problem", which can be found at the address
Statement of the \problem:
Solve for all solutions $a,b,c$ over the natural numbers to the relation
\begin{equation}
\Big(1 + \frac{1}{a}\Big) \Big(1 + \frac{1}{b}\Big) \Big(1 + \frac{1}{c}\Big) = 2 \,.\label{eq:OriginalRelation}
\end{equation}
I offer a simpler problem with solution that's more my limited mathematical ability.
My solution to the problem Solution to this problem.
This next problem (#11) is found on the YouTube channel Presenter: SyberMath, titled 'Solving A Differential Equation $|$ Two Methods', which can be found at the address
Statement of the problem:
Solve for $y$ as a function of $x$ given the relation
\begin{equation}
\left(\frac{dy}{dx}\right)^2 - 1 = x^2.
\end{equation}
I offer an alternative solution that employs the unipodal algebra and hyperbolic trig functions.
My solution to the problem Solution to this problem.
This next problem (#12) is found at:
Titled: Solving a Quick and Easy Functional Equation
By presenter: SyberMath
Statement of the problem:
Solve for $f(x)$ as a function of $x$ given the relation
\begin{equation}
f(x + \sqrt{x^2 + 1}) = \frac{x}{x + 1}\,.
\end{equation}
I offer an alternative solution that employs hyperbolic trig functions.
My solution to the problem Solution to this problem.
This problem (#13) is found on the YouTube channel MindYourDecisions, from
Statement of the problem:
Solve for real values of $x$ in the following equation:
\begin{equation}
\left(x - \frac{1}{x}\right)^{1/2} + \left(1 - \frac{1}{x}\right)^{1/2} = x\,.
\end{equation}
My solution is found here Solution to this problem.
This problem (#14) is found on the YouTube channel Spencer's Academy, from
Statement of the problem:
Solve for real values of $x$ in the following equation:
\begin{equation}
(4 + \sqrt{15})^x + (4 - \sqrt{15})^x = 62\,.
\end{equation}
My solution is found here Solution to this problem.
This problem (#15) is found on the YouTube channel ?, from
Given the relation
\begin{equation}
a + \frac{1}{a} = 7\,,\label{eq:TheGiven}
\end{equation}
where $a$ is a positive real number, find
\begin{equation}
\sqrt{a} + \frac{1}{\sqrt{a}}\,,
\end{equation}
and
\begin{equation}
\sqrt{a} - \frac{1}{\sqrt{a}}\,.
\end{equation}
My solution is found here Solution to this problem.
This problem (#16) is found on the YouTube channel dy d Oscar, from
https://www.youtube.com/watch?v=A-SFQ0s4qQw
Titled: This Oxford Integral Question STUMPED Students
Given the relation
\begin{equation}
6 + f(x) = 2f(-x) +3x^2 \int_{-1}^1\! f(t) dt\,,
\end{equation}
we are asked to find the value of the integral
My solution is found here Solution to this problem.
This problem (#17) [Unipodal]:
The YouTube video is found at [Unipodal]:
By presenter: Math is math
Given the relations
\begin{align}
x + y &= 19 \,,\\
x y &= 9 \,,
\end{align}
find
\begin{equation}
x \sqrt{x}+y \sqrt{y}\,,
\end{equation}
where $x,y$ are positive real numbers.
Problem 18:
The YouTube video is found at [Unipodal]:
Given the relations
\begin{align}
x^5 + y^5 &= 152 \,,\\
x + y &= 2 \,,
\end{align}
find all solutions for $x,y$ over the complex numbers.
Problem 19:
The YouTube video is found at [Unipodal]:
Given the relation
\begin{equation}
\sqrt[3]{x+49} + \sqrt[3]{x-49} = 2 \,,\label{eq:TheGiven1}\\
\end{equation}
solve for $x$ over the complex numbers.
Problem 20:
The YouTube video is found at [Unipodal]:
Given the relation
\begin{align}
x^2 - y^2 &= \sqrt{10} \,,\\
xy &= \sqrt{10} \,,
\end{align}
solve for $x+y$ over the complex numbers.
Problem 21:
The YouTube video is found at [Unipodal]:
Given the relations
\begin{align}
p + q &= 8 \,,\\
pq &= 20 \,,
\end{align}
solve for $p$ and $q$ over the complex numbers.
Problem 22:
The YouTube video is found at [Unipodal]:
Given the relations
\begin{align}
\sqrt{x} + \sqrt{y} &= 5 \,,\\
\sqrt{x+16} - \sqrt{y+5} &= 2 \,,
\end{align}
solve for $x$ and $y$ over the real numbers.
Problem 23:
The YouTube video is found at [Unipodal]:
Given the relations
\begin{align}
\sqrt{x} + \sqrt{y} &= 7 \,,\\
x - y &= 7 \,,
\end{align}
solve for $x>0$ and $y>0$ over the real numbers.
Problem 24 [Unipodal]:
The YouTube video is found at [Unipodal]:
Given the relations
\begin{align}
x^2+ y^2 &= 7 \,,\\
x^3+ y^3 &= 10\,,
\end{align}
solve for $x+y$ over the real numbers.
Problem 25 [Unipodal]:
The YouTube video is found at :
Simplify the expression
\begin{equation}
(208 + 120\sqrt{3})^{1/6}
\end{equation}
over the real numbers.
Problem 26 [Unipodal]:
The YouTube video is found at:
Given the relation
\begin{equation}
a^4 + b^4 = 10a^2b^2\,,
\end{equation}
find the value of
\begin{equation}
\frac{a+b}{a-b} \,,
\end{equation}
over the real numbers.
Problem 27 [Unipodal]:
The source of this \problem\ is from G.\ Sobczyk's book (\cite{Sobczyk}, p.\ 36),
\bibitem{Sobczyk}G.\ Sobczyk, {\it New Foundations in Mathematics, The Geometric
Given the relation
\begin{equation}
z^n + \frac{1}{z^n}= \beta\,,
\end{equation}
find the value of $z$. (This special equation was called the
Problem 28 [Unipodal]:
The YouTube video is found at:
Given the relation
\begin{equation}
x + \frac{1}{x}= -1\,,
\end{equation}
find the value of
\begin{equation}
x^{25} + \frac{1}{x^{25}}=\ ?
\end{equation}
Problem 29 [Unipodal]:
The YouTube video is found at:
Simplify the expression
\begin{equation}
\left( \frac{1+\sqrt{5}}{2} \right)^{12}\,.
\end{equation}
Problem 30 [Unipodal]:
The source of this problem is inspired from a test problem from
Given the relations
\begin{align}
a + b &= 2\,,\\
a^3 + b^3 &= 6\,,
\end{align}
find the value of
\begin{equation}
a^3 - b^3 \,.
\end{equation}
Problem 31 [Unipodal]:
This problem was inspired by the YouTube video is found at:
Given the relations
\begin{align}
x - y &= 10\,,\\
xy &= -20\,,
\end{align}
find the value of
\begin{equation}
\frac{1}{x} + \frac{1}{y} \,.
\end{equation}
Problem 32 [Not Unipodal]:
This problem is from the YouTube video:
Given the relation
\begin{equation}
x^x = 2^{8+2x} \,,
\end{equation}
find the value of $x$.
Problem 33 [Not Unipodal]:
This problem was inspired by recent `olympiad' problems.
Perform the indefinite integral.
\begin{equation}
I = \int \ln (x+\sqrt{1+x^2}) dx \,.
\end{equation}
Problem 34 [Not Unipodal]:
Given the relations
\begin{equation}
6\log a = 4\log b = 3\log c \,.
\end{equation}
find the numeric value of
\begin{equation}
\log_{ab} c\,.
\end{equation}
Problem 35 [Not Unipodal]:
Given the relation
\begin{equation}
b^3 - b = 1\,.
\end{equation}
find
\begin{equation}
b^5 - b^4 \,.
\end{equation}
Problem 36 [Not Unipodal]:
Given the relation
\begin{equation}
6!\times 7! = x!\,,
\end{equation}
find $x$.
Problem 37 [Not Unipodal]:
If $n$ is a positive integer, show that (I changed the problem slightly.)
\begin{equation}
\frac{n}{6} + \frac{n^2}{2}+ \frac{n^3}{3}\label{eq:TheExpression}
\end{equation}
is also a positive integer.
Problem 38 [Not Unipodal]:
Simplify the following radical.
\begin{equation}
R = \sqrt{a + \sqrt{a^2-1}} \,.
\end{equation}
Problem 39 [Not Unipodal]:
Given the relations
\begin{align}
5^x + 5^y &= 15750\,,\\
x + y &= 9\,,
\end{align}
find the value of $x$ and $y$.
Problem 40 [Not Unipodal]:
Given the relation
\begin{equation}
x^{\log_3 x} = 81\,,
\end{equation}
find the value of $x$.
Problem 41 [Unipodal]:
The YouTube video is found at:
Given the relation
\begin{equation}
(x+9)^4 + (x+11)^4 = 706\,,
\end{equation}
find the value of $x$.
Problem 42 [Unipodal]:
This problem is one I adapted from one I saw recently on YouTube
Given the relations
\begin{align}
\sqrt{a} + \sqrt{b} &= \sqrt{31}\,,\\
\sqrt{ab} &= 2\,,
\end{align}
find the value of $ \sqrt{a} - \sqrt{b} $, where $a,b>0$.
Problem 43 [Not Unipodal]:
Given the relation
\begin{equation}
2^x\cdot 3^{x^2} = 6\,,
\end{equation}
find the values of $x$.
Problem 44 [Not Unipodal]:
Given the relation
\begin{equation}
\frac{(x+7)!}{(x+3)!} = 7920\,,
\end{equation}
find the value of $x$.
Problem 45 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
(x+2)^4 + (x+1)^4 = 17\,,
\end{equation}
find the real values of $x$.
Problem 46 [Unipodal]: [This is an elegant solution that I stumbled upon. Enjoy.]
This problem on YouTube at
Given the relations
\begin{align}
x^5 + y^5 &= 152\,,\\
x+y &= 2\,,
\end{align}
find the values of $x,y$
Problem 47 [Unipodal]:
This problem on YouTube at
Given the relations
\begin{align}
4^x - 4^y &= 24\,,\\
2^{x+y} &= 35\,,
\end{align}
find the values of $x-y$.
Problem 48 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
(x-6)^4 + (x-8)^4=16 \,,
\end{equation}
find the values of $x$.
Problem 49 [Unipodal]:
This problem on YouTube at
Given the relations
\begin{align}
a^2 - b^2 -(a-b) &= 6\,,\\
2ab- (a+b) &= 17\,,
\end{align}
find the values of $a,b$ in the real numbers.
Problem 50 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
\sqrt[4]{x} + \sqrt[4]{97 - x} = 5 \,,
\end{equation}
find the values of $x$.
Problem 51 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
(5x-6)^2 + (10-5x)^3 = 16 \,,
\end{equation}
find the values of $x$.
Problem 52 [Not Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
(x+\sqrt{1+x^2}) (y+\sqrt{1+y^2}) = 1 \,,
\end{equation}
find the values of $ (x+y)^2$.
Problem 53 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
(z + 1)^5 = (z - 1)^5 \,,
\end{equation}
find the values of $z$.
Problem 54 [Not Unipodal]:
This problem on YouTube at
Given the relations
\begin{align}
\log y &= \log_x (2x-5)\,,\\\
\log x &= \log_y (x+15)\,,
\end{align}
find the values of $x,y$.
Problem 55 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
\sqrt{x+\sqrt{x}} + \sqrt{x-\sqrt{x}}= \sqrt{6} + \sqrt{2} \,,
\end{equation}
find the values of $x$.
Problem 56 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
(\sqrt{2}+ 1)^x + (\sqrt{2} - 1)^x = 34 \,,
\end{equation}
find the values of $x$.
Problem 57 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
\big(7 + \frac{1}{x}\big)^4 - \big(5 + \frac{1}{x}\big)^4 = 240 \,,
\end{equation}
find the real values of $x$.
Problem 58 [Unipodal]: [alternative solution]
This problem on YouTube at
Given the relation
\begin{equation}
\big(7 + \frac{1}{x}\big)^4 - \big(5 + \frac{1}{x}\big)^4 = 240 \,,
\end{equation}
find the real values of $x$.
Problem 59 [Not Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
6^x + 9^x = 2^{2x+1} \,,
\end{equation}
find the integer values of $x$. [As I saw no requirement to treat $x$
Problem 60 [Unipodal]: [introduces using imaginary numbers from the start]
This problem on YouTube at
Given the relation
\begin{equation}
x^2 - 2 = \sqrt{x+2} \,,
\end{equation}
find the values of $x$.
Problem 61 [Not Unipodal]:
This problem on YouTube at
Let $a$ be a positive real number. Then, if
\begin{equation}
a^2 - 17a = 16\sqrt{a} \,,
\end{equation}
find the values of
\begin{equation}
\sqrt{a-\sqrt{a}} \,.
\end{equation}
Problem 62 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
(x - x^3)^{1/2} + (x^2 - x^3)^{1/2} = 1 \,,
\end{equation}
find the values of $x$.
Problem 63 [Unipodal]:
This problem on YouTube at
Given the relations
\begin{align}
x^4 -y^4 &= 16\,,\\
xy &= 2\,,
\end{align}
find the values of $x,y \in Reals$.
Problem 64 [Not Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
\sqrt{x+4} + \sqrt{-x-4} = 4 \,,
\end{equation}
find the values of $x$ over the complex numbers.
Problem 65 [Unipodal]:
This problem on YouTube at
Given the relations
\begin{align}
3^x -3^y &= 16\,,\\
3^{x+y} &= 4\,,
\end{align}
find the values of $x,y \in$ Reals.
Problem 66 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
(\sqrt{10}+3)^{x} + (\sqrt{10}-3)^{x} = 38 \,,
\end{equation}
find the values of $x$.
Problem 67 [Unipodal]:
This problem on YouTube at
This has been one of the most revealing problems on the nature
Given the relation
\begin{equation}
\sqrt{x}+\sqrt{x+1}+\sqrt{x+2} = \sqrt{x+7}\,,
\end{equation}
find the values of $x$.
Problem 68 [Not Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
2^a+2^b+2^c = 148 \,,
\end{equation}
find the integer values of $a,b,c$.
Problem 69 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
\sqrt{2}+\sqrt{x} = 2\,,
\end{equation}
find the values of $x$.
Problem 70 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
\left( \frac{x+1}{x}\right)^2 - \left( \frac{x+1}{x-1}\right)^2 = 1\,,
\end{equation}
find the values of $x$.
Problem 71 [Not Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
K^2 = 8 i\,,
\end{equation}
find the values of $K$.
Problem 72 [Not Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
a^2 + 2ab + b = 44\,,
\end{equation}
find the positive integer values of $a,b$. I will add to this the constraint
that
\begin{equation}
a + b \le 10\,.
\end{equation}
Problem 73 [Unipodal]:
This problem on YouTube at
Given the relations
\begin{equation}
x^2 - y^2 = 24\,,\
\end{equation}
and
\begin{equation}
xy = 35\,,
\end{equation}
find the solutions to $x,y$.
Problem 74 [Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
x^2 + \left( \frac{3x}{x-3}\right)^2 = 16\,,
\end{equation}
find the values of $x$.
The following is a conventional solution:
\begin{equation}
-\left(\frac{3x}{x-3}\right)^2 = x^2-16 \,.
\end{equation}
On multiplying this out and placing the result into standard form, we get
\begin{equation}
x^4 - 6x^3 + 2x^2 + 96x - 144 = 0 \,.
\end{equation}
And WolframAlpha.com claims the solutions are
\begin{align}
x &= 4\pm2\sqrt{2}\, i\,, \\
x &= -1\pm\sqrt{7}\,.
\end{align}
*Unipodal solution in preparation*.
Problem 75 [Not Unipodal]:
This problem on YouTube at
Given the relation
\begin{equation}
x-3\sqrt{x} = 1\,,
\end{equation}
find the value of the objective function
\begin{equation}
x^2 + \frac{1}{x^2}\,.
\end{equation}
Problem 76 [Unipodal]:
This problem on YouTube at
Given the relations
\begin{align}
x + y &= 1\,,\\
xy &= 1\,,
\end{align}
find the values of $x,y$.
Problem 77 [Unipodal]:
This problem is by
This is a problem I made up, and is similar
Problem 78 [Not Unipodal]:
This problem is by
Find the value of $(\sqrt{2}-1)^{10}$.
Note: I think it helps to know a few lines of Pascal's Triangle.
Problem 79 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\frac{5}{x} \frac{5}{x} = \frac{x}{5}\,,
\end{equation}
find the values of $x$.
Problem 80 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
2^x + 4^x + 8^x = 155\,,
\end{equation}
find the values of $x$.
Problem 81 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
(x-5)^{\log (5x-25)} = 2\,,
\end{equation}
find the values of $x$.
Problem 82 [Not Unipodal]:
This problem is by
Find the value of
\begin{equation}
8^5 + 8^4 + 8^3 + 8^2 + 8^1 + 8^0\,.\
\end{equation}
Problem 83 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{\sqrt{x}} = 3\,,
\end{equation}
find the values of $x$.
Problem 84 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
a^4 = (a-1)^4\,,
\end{equation}
find the values of $a$.
Problem 85 [Not Unipodal]:
This problem is by
Given the relations
\begin{align}
\sqrt{x} + y &= 7\,,\\
x + \sqrt{y} &= 11\,,
\end{align}
find the values of $x,y \in$ Reals.
Problem 86 [Unipodal]:
This problem is by
Given the relations
\begin{align}
\log x + \log y &= 5\,,\\
\log x \cdot \log y &= 5\,,
\end{align}
find the values of $x,y$.
Problem 87 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{2}^{\sqrt{m}} - \sqrt{2}^{\sqrt{n}} = 32,768\,,
\end{equation}
find the values of $m,n$ as integers.
Problem 88 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
81^{\sin^2 x} + 81^{\cos^2 x} = 30\,,
\end{equation}
find the values of $x$ in (radians) between 0 and $2\pi$.
Problem 89 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{1+ \sqrt{\strut1+x}} = \sqrt[3]{x}\,,
\end{equation}
find the values of $x$.
Problem 90 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{\strut x-1} + \sqrt{\strut x+2} = 3\,,
\end{equation}
solve for $x$ values.
Problem 91 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
(x + 100)^2 = 2x + 199\,,
\end{equation}
find the values of $x$.
One possible substitution is to set $y=x+100$ (which exposes
Problem 92 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x + y &= 1\,,\\
x^4 + y^4 &= 881\,,
\end{align}
find the value of $xy$.
Problem 93 [Not Unipodal]:
This problem is by
\begin{equation}
\frac{(1+i)^{2024}}{(1-i)^{2023}}\,.\label{eq:Given.Expression}
\end{equation}
Problem 94 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^6 + \frac{1}{x^6} = 488\,,
\end{equation}
solve for the values of
\begin{equation}
k = x + \frac{1}{x} \,,
\end{equation}
for $x$ over the positive reals.
Problem 95 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
20^k\cdot 50^k = 8\,,
\end{equation}
find the values of $k$.
Problem 96 [Unipodal]:
This problem is by
Given the relations
\begin{align}
6^x +6^y &= 42\,,\\
x + y &= 3\,,
\end{align}
find the values of $x,y$.
Problem 97 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
x = \cuberoot{7+\sqrt{50}} + \cuberoot{7-\sqrt{50}} \,,
\end{equation}
solve for the (real) values of $x$ more simply.
Problem 98 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
9^{x+1} - 9^{x-1} = 20\,,
\end{equation}
solve for the (real) values of $x$.
Problem 99 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\left(\frac{2}{3}\right)^x + \left(\frac{3}{2}\right)^x = 4\,,
\end{equation}
find the values of $x$.
Problem 100 [Unipodal]:
This problem is by
Given the relations
\begin{align}
\log_yx + \log_xy &= \frac{26}{5}\,,\\
x y &= 64\,,
\end{align}
find the values of $x,y$ in the positive reals.
Problem 101 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
5^x +35^{x/2} = 7^x\,,
\end{equation}
find the values of $x$.
Problem 102 [Not Unipodal]:
This problem is by
Given the relations
\begin{align}
x^2 + xy + y^2 &= 96\,,\\
x + \sqrt{xy} + y &= 16\,,
\end{align}
find the values of $x,y \in$ Reals.
Problem 103 [Unipodal]:
This problem is by
Given the relations
\begin{align}
a + b^{-1} &= 4\,,\\
a^{-1} + b&= \frac{16}{15}\,,
\end{align}
find the values of $ab$.
Problem 104 [Not Unipodal]:
This problem is by
Find the value of the following definite integral:
\begin{equation}
\int_0^1 \ln (1 + x^2) dx\,.
\end{equation}
Problem 105 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{x+7} - \sqrt{x-9} = 2\,,
\end{equation}
find the values of $x$.
Problem 106 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\frac{x}{y} + \frac{y}{x} = 1\,,
\end{equation}
find the value of
\begin{equation}
\left(\frac{x}{y}\right)^{153} + \left(\frac{y}{x}\right)^{153} = z\,,
\end{equation}
where $z$ is introduced now for convenience.
Problem 107 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
4^{x+1} - 4^{x-1} = 25\,,
\end{equation}
find the values of $x$.
Problem 108 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{x} y^{y} = 8 x^{y} y^{x}\,,
\end{equation}
find the smallest positive integer values of $x,y$ with $x>y$.
Problem 109 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{3/2} = 3^{3/2}\,,
\end{equation}
find the values of $x$.
Problem 110 [Unipodal]:
Given the relations
\begin{align}
x^2 + y^2 &= 6\,,\\
x + y &= 3\,,
\end{align}
find the value of $x^{-1} - y^{-1}$.
Problem 111 [Not Unipodal]:
This problem is by
Given the relations
\begin{align}
x^2 + xy + x &= 10\,,\\
y^2+ xy + y &= 20\,,
\end{align}
find the values of $x,y$.
Problem 112 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x + y &= 4\,,\\
x^5 + y^5 &= 464\,,
\end{align}
find the value of $x,y$.
Problem 113 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{\strut\frac{\strut 4^{20} - 2^{21} + 1}{\strut 2^{20} + 2^{11} + 1}} = 2^{x} - 1\,,
\end{equation}
find the values of $x$.
Problem 114 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
m^2 - m^3 = 36\,,
\end{equation}
find the values of $m$
Problem 115 [Unipodal]:
This is one of my favorite problems so far. I solved it
This problem is by
Given the relations
\begin{align}
4 x^2 - 4y^2 &= 1\,,\\
4xy &= 1\,,
\end{align}
find the real values of $x+y$.
Problem 116 [Unipodal]:
This is one of my favorite problems so far. I solved it
This problem is by
Given the relation
\begin{equation}
x^2 = (5 - \sqrt{24})^x\,,
\end{equation}
find the values of $x \in$ Reals.
Problem 117 [Unipodal]:
This is one of my favorite problems so far. I solved it
This problem is by
Given the relation
\begin{equation}
\sqrt{3+\sqrt{x+9}} = \cuberoot{x}\,,\
\end{equation}
find the values of $x \in$ the positive reals.
Problem 118 [Not Unipodal]:
This problem is by
Given the relations
\begin{align}
\sqrt{a} + \sqrt{2-b} &= \sqrt{2}\,,\\
\sqrt{b} + \sqrt{2-a} &= \sqrt{2}\,,
\end{align}
find the values of $a,b$.
Problem 119 [Unipodal]:
This problem is by
Given the relations
\begin{align}
a^2 - ab &= 14\,,\\
b^2 + ab &= 60 \,,\
\end{align}
find the values of $a,b$.
Problem 120 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
(x+11)^4 - (x+9)^4 = 80\,,
\end{equation}
find the values of $x \in$ Reals.
Problem 121 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x + y &= 1\,,\\
xy &= 1\,,
\end{align}
find the real values of $x,y$.
Problem 122 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^2 = 4^x\,,
\end{equation}
find the real values of $x$.
Problem 123 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{x^{x^3}} = 3\,,
\end{equation}
find the real values of $x$.
Problem 124 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{x^{2}} = 16\,,
\end{equation}
find the real values of $x$.
Problem 125 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x = \frac{15}{ 2+ \frac{15}{2+ \frac{15}{ 2+\frac{15}{\cdots}}}}\,,
\end{equation}
find the real values of $x$.
Problem 126 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x &= \frac{\sqrt{7} + \sqrt{3}}{\sqrt{7} - \sqrt{3}}\,,\\
y &= \frac{\sqrt{7} - \sqrt{3}}{\sqrt{7} + \sqrt{3}}\,,
\end{align}
find the values of
\begin{equation}
x^4 + y^4 \,,
\end{equation}
over the reals.
Problem 127 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\frac{2^{33}+2^{22}+2^{11}}{2^{33}-1}\,,
\end{equation}
find its value.
Problem 128 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{x^6} = \sqrt{2}^{\sqrt{2}}\,,
\end{equation}
find the values of $x$.
Problem 129 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x - y &= 4\,,\\
x^3 - y^3 &= 28\,,
\end{align}
find the values of $x,y$.
Problem 130 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^2 - x +1 = 0\,,
\end{equation}
find the values of
\begin{equation}
x^{2020} + x^{1010} - 1\,.
\end{equation}
Problem 131 [Unipodal]:
This problem is by
Given the relations
\begin{align}
3^{x-4}+ 3^{y-4} &= 244\,,\\
x+y &= 13\,,
\end{align}
find the values of $x,y$.
Problem 132 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\frac{16}{x} - \frac{8}{x^2} + \frac{4}{x^3}
- \frac{2}{x^4} + \frac{4}{x^5} = 32\,,
\end{equation}
find the values of $x$.
Problem 133 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x + \sqrt{x} = x\sqrt{x}\,,
\end{equation}
find the values of $x$ over the positive reals.
Problem 134 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
x + \frac{1}{x} = \sqrt{3}\,,
\end{equation}
solve for the values of
\begin{equation}
x^{50} + \frac{1}{x^{50}} \,.
\end{equation}
Problem 135 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{\log 27} + 9^{\log x} = 36\,,
\end{equation}
find the values of $x$ over the real numbers.
By the way, I interpret the logarithm as being in base 10.
Problem 136 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
64^{x} = x^{192} \,,
\end{equation}
find the values of $x$ over the real numbers.
Solution to this problem.
Problem 137 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
25^{2x} = 50 \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 138 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\left(\frac{x}{5}\right)^x = 5^{5^2} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 139 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
a + \frac{1}{a} =6 \,,
\end{equation}
find the values of
\begin{equation}
a - \frac{1}{a}\,.
\end{equation}
Problem 140 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
4^x + 25^x = 10^{x+1} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 141 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
3^{3x-3x^2} = x^2 - x \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 142 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
a = \sqrt{5} + \sqrt{6} \,,
\end{equation}
find the values of the following expression over the real numbers.
\begin{equation}
a^2 + \frac{1}{a^2}\,.
\end{equation}
Problem 143 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{x} = 4^{4+ x} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 144 [Unipodal]: (One of my favorites!)
This problem is by
Given the relations
\begin{align}
a^2 + b^2 &= 7\,,\\
a^3 + b^3 &= 10\,,
\end{align}
find the values of $a + b$.
Problem 145 [Not Unipodal]:
This problem is by
\begin{equation}
\left(\frac{x}{5}\right)^{x} = 5^{5^2} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 146 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{\sqrt{x}} = 4^{2} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 147 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x^2 + y^2 &= 61\,,\\
x-y &= 11\,,
\end{align}
find the values of $x,y$.
Problem 148 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{x^{1+x}} = 256 \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 149 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
2^x - 9^x = \sqrt{18^x-81^x} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 150 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\cuberoot{x} + \sqrt{x} = \frac{4}{27} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 151 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x^2 - y^2 &= 27\,,\\
xy &= 18\,,
\end{align}
find the values of $x+y$.
Problem 152 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{x} - \sqrt{x-2} = 1 \,,
\end{equation}
find the values of $x$.
Problem 153 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{\cuberoot{33+x}} + \sqrt{\cuberoot{32-x}} = 3 \,,
\end{equation}
find the real values of $x$
Problem 154 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x^5 + y^5 &= 152\,,\\
x + y &= 2\,,
\end{align}
find the values of $x,y$.
Problem 155 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
(\sqrt{10}+3)^x + (\sqrt{10}-3)^x = 38\,,
\end{equation}
find the values of $x$.
Problem 156 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{ \sqrt{x}} = 10 \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 157 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\obz + 2|z| = 13 - 4i \,,
\end{equation}
find the values of $z$ over the complex numbers.
Problem 158 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\obz + z|z| = 24- 12i \,,
\end{equation}
find the values of $z$ over the complex numbers.
Problem 159 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sin x + \cos x = \frac{1}{5}\,,
\end{equation}
find the values of $\tan x$ where \((0 < x < \pi)\).
Problem 160 [Unipodal]:
This problem is by
Given the relations
\begin{align}
a^2 + b^2 &= 74\,,\\
ab &= 35\,,
\end{align}
find the values of $a,b$.
Problem 161 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{-x^x} = 2^{\sqrt{2}} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 162 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\phi = \left(\frac{1-i}{1+i} \right)^2 + \left(\frac{1-i}{1+i} \right)^3 + \left(\frac{1-i}{1+i} \right)^4 \,,
\end{equation}
find the values of $\phi$ over the complex numbers.
Problem 163 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
2^{x} - 9^x = \sqrt{ 18^{x} - 81^x} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 164 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{x+7} - \sqrt{x-9} = 2\,,
\end{equation}
find the values of $x$
Problem 165 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\log_2 x= \log_x4 \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 166 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x^2 + y^2 &= 61\,,\\
x - y &= 11\,,
\end{align}
find the values of $x,y$.
Problem 167 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\tan z = -\frac{3i}{5}\,,
\end{equation}
find the values of $z$.
Problem 168 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
x = \sqrt{x -\frac{1}{x}} + \sqrt{1 -\frac{1}{x}}\,,
\end{equation}
Problem 169 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{x} = 3^{2x+27} \,,
\end{equation}
find the values of $x$ over the real numbers
Problem 170 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{7} + \frac{1}{x^{7}} = 6 \,,
\end{equation}
what is
\begin{equation}
\phi = x^{21} + \frac{1}{x^{21}}\,?
\end{equation}
Problem 171 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\ln \big(iz + \sqrt{1 - z^2} \big) = \frac{i\pi}{3}\,,
\end{equation}
find the values of $z$ over the real numbers.
Problem 172 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\frac{b+ai}{a+bi} = \frac{4+i}{1+4i} \,,
\end{equation}
find the values of $a,b$ over the real numbers.
Problem 173 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relations $z=a+bi$ and
\begin{equation}
(a+bi)^2 = b+ia\,,
\end{equation}
find the values of $z$.
Problem 174 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\frac{3}{9^{-x}} + \frac{10}{6^{-x}}= 4^{x} \,,
\end{equation}
find the real values of $x$.
Problem 175 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relations $z=a+bi = re^{i\theta}$ and
\begin{equation}
z^{14} = \obz\,,
\end{equation}
find the values of $z$.
Problem 176 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relations
\begin{equation}
\left|\frac{z}{z + 2}\right| = 3\,,
\end{equation}
find the values of $x,y$ in $z = x + iy$.
Problem 177 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relations
\begin{equation}
z^z= e^{\textstyle-\frac{\pi}{2}}\,,
\end{equation}
find the real values of $z$
Problem 178 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z = i^z\,,
\end{equation}
find the complex values of $z$.
Problem 179 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\phi =\left( \frac{1+\sqrt{3} i }{1-\sqrt{3} i} \right)^{10}\,,
\end{equation}
simplify.
Problem 180 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z + 2\obz = \frac{ 2-i }{1+3 i}\,,
\end{equation}
find the complex values of $z$.
Problem 181 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z i^z = 4\,,
\end{equation}
find the complex values of $z$.
Problem 182 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{9-x^2} + \sqrt{4-x^2} = 4\,,
\end{equation}
find the real values of $x$.
Problem 183 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\frac{1}{z} + \frac{1}{\obz} = 4\,,
\end{equation}
find the complex values of $z$ (locus of points).
Problem 184 [Not Unipodal, Complex Numbers]:
Pending completion.
Problem 185 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
i^{z+i} = 1\,,\
\end{equation}
find the complex values of $z$.
Problem 186 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{\log 64} + 4^{\log x} = 10\,,
\end{equation}
find the values of $x$.
Problem 187 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
z^{z^{z+1}} = 4\,,
\end{equation}
find the values of $z$
Problem 188 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
e^x + x + 1=0\,,
\end{equation}
find the values of $x$.
Problem 189 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
|z| = |z-i|\,,\
\end{equation}
find the values of $z$.
Problem 190 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
Problem 191 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
W(e^{e^2+1+x^x}) = x^x\,,
\end{equation}
find the values of $x$.
Problem 192 [Unipodal]:
This problem is by
Given the relations
\begin{align}
4^x - 4^y&= 24\,,\\
2^{x + y} &= 35\,,
\end{align}
find the real values of $\phi=x-y$.
Problem 193 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x+y&= 7\,,\\
x y &= 7\,,
\end{align}
find the values of $x,y$.
Problem 194 [Not Unipodal]:
This problem is by
Given the relations
\begin{equation}
x^x = 2^{8+2x}\,,
\end{equation}
find the values of $x$.
Problem 195 [Not Unipodal]:
This problem is by
Given the relations
\begin{align}
\sqrt{x^n} + \sqrt{y^n} &= 13\,,\\
{x^n} - {y^n} &= 13\,,
\end{align}
find the positive integer values of $n,x,y$.
Problem 196 [Not Unipodal: the first word problem in the set]:
This problem is by
Solve the word problem:
If you're interested, see my many articles on solving algebra
word problems at:
Problem 197 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\frac{x}{y} + \frac{ y}{ x} = 1\,,
\end{equation}
find the value of
\begin{equation}
\phi = \left( \frac{x}{y}\right)^{153}+ \left(\frac{ y}{ x}\right)^{153}\,.
\end{equation}
Problem 198 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z = \obz^2 + 1\,,
\end{equation}
find the values of $z$.
Problem 199 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
|z+w| = |z-w|\,,
\end{equation}
find the values of
\begin{equation}
\phi = \arg{z} - \arg{w} \,.
\end{equation}
Problem 200 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{x} + \sqrt{x-12} = 4\,,
\end{equation}
find the real values of $x$.
Problems 201-203 [Pending]
Problem 204 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x = \sqrt{x}^{\sqrt{x}} \,,
\end{equation}
find the values of $x$.
Problem 205 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relations
\begin{align}
z+ \obz &= 2\,,\\
z\obz &= |z| + 2\,,
\end{align}
Problem 206 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
w = (a+bi)^4 + (b+ai)^4\,,
\end{equation}
is $w$ a real number?
Problem 207 [Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z = \sqrt{2+i}\,,
\end{equation}
express $z$ without the square root sign.
Problem 208 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x+y&= 4\,,\\
x^5+y^5 &= 464\,,
\end{align}
find the values of $x,y$.
Problem 209 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z^{|z|} = \frac{1+\sqrt{3} i}{2}\,,
\end{equation}
find the values of $z$.
Problem 210 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z^2 = |z|\,,
\end{equation}
find the values of $z$.
Problem 211 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\obz + i = z i\,,
\end{equation}
find the values of $z$.
Problem 212 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\frac{z}{|z|} = \obz + i \,,
\end{equation}
find the values of $z$.
Problem 213 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{\log_5 3} = \sqrt{x} + 4 \,,
\end{equation}
find the values of $x$.
Problem 214 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{2x^6} = 3 \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 215 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
9^{4^m} = 4^{9^m} \,,
\end{equation}
find the values of $m$ over the real numbers.
Problem 216 [Unipodal: Complex Numbers]:
This problem is by
Given the relations
\begin{align}
z + w &= 4\,,\\
z^3+ w^3 &= 4\,,
\end{align}
find the values of $z,w$.
Problem 217 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\frac{\sin\theta}{1-\cos\theta} = i \,,
\end{equation}
find the values of $\theta$
Problem 218 [Not Unipodal]:
This problem is by
Given the relations
\begin{align}
x^{\log y}+ y^{\log x} &= 2\,,\\
x^{\log x}+ y^{\log y}&= 11\,,
\end{align}
find the values of $x,y$. (Note, $x,y>0$)
Problem 219 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
z^z = i \,,
\end{equation}
find the values of $z$.
Problem 220 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
y^{y^4}= 64 \,,
\end{equation}
find the values of $y$.
Problem 221 [Not Unipodal: Complex numbers]:
This problem is by
Given the relation
\begin{equation}
\frac{z-1}{\Re(z)+1} = i\,,
\end{equation}
find the values of $z$.
Problem 222 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
2^x = x^{32}\,,
\end{equation}
find the values of $x$.
Problem 223 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\phi= (1+i)^n + (1-i)^n\,,
\end{equation}
find a simpler form for $\phi$.
Problem 224 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z^{|z|}= 2+2\sqrt{3}\, i\,,
\end{equation}
find the values of $z$.
Problem 225 [Unipodal]:
This problem is by
Given the relations
\begin{align}
a+b &= -2\,,\\\
a^3+b^3 &= -56\,,
\end{align}
find the values of $a,b$.
Problem 226 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{\log 27} + 9^{\log x}=36\,,
\end{equation}
find the values of $x$.
Problem 227 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x^6 + y^6 &= 793\,,\\
x^3+ y^3 &= 35\,,
\end{align}
find the values of $x,y$.
Problem 228 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z^{z}= i\,,
\end{equation}
find the values of $z$.
Problem 229 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z^4= \obz\,,
\end{equation}
find the values of $z$.
Problem 230 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
|z^2 - 1| = |z|^2\,,
\end{equation}
find the values of $z$ (locus of points in the $x,y$ plane).
With apologies, I accidentally changed the problem a bit, as you can see.
Problem 231 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{x^2} = 2^{1024}\,,
\end{equation}
find the values of $x$.
Problem 232 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{x+a} + \sqrt{x}= a\,,
\end{equation}
find the value of
\begin{equation}
\phi = \sqrt{x+a} - \sqrt{x}\,.
\end{equation}
Problem 233 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^{ \sqrt{x}} = 10 \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 234 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
256^{x} = \frac{1}{x} \,,
\end{equation}
find the values of $x$ over the real numbers.
Problem 235 [Unipodal and Conventional]:
This problem is by
Given the relation
\begin{equation}
x^2 = (5-\sqrt{24})^x\,,
\end{equation}
find the real values of $x$.
Problem 236 [Not Unipodal, and some useful Lambert $W$ function lemmas]:
This problem is by
Given the relation
\begin{equation}
x^{5} = 9^x \,,
\end{equation}
find the values of $x$ over the real (or complex) numbers.
Problem 237 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
a^3 + b^3 + 3ab = 1 \,,
\end{equation}
find the values of $a+b$ over the real numbers.
Problem 238 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z^{|z|^2}=2i\,,
\end{equation}
find the values of $z$.
Problem 239 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
z|z-1|=20+20i\,,
\end{equation}
find the values of $z$.
Problem 240 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
(1+i\tan\theta)^5 = 32\,,
\end{equation}
find the values of $\theta$.
Problem 241 [Not Unipodal, Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
e^{x^2-1} = x\,,
\end{equation}
find the values of $x$.
Problem 242 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
e^{x} = \ln x\,,
\end{equation}
find the values of $x$.
Problem 243 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{x}^x = 2^{ x+16}\,,
\end{equation}
find the values of $x$.
Problem 244 [Unipodal]:
This problem is by
Given the relation
\begin{equation}
\left(\frac{n}{n-1}\right)^2 + \left(\frac{n}{n+1}\right)^2 = \frac{10}{9}\,,
\end{equation}
find the real values of $n$.
Problem 245 [Unipodal]:
This problem is by
Given the relations
\begin{align}
x^2 - y^2 &= 40\,,\\
xy &= 99\,,
\end{align}
find the values of $\phi = x+y$.
Problem 246 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
x^4 = 3^{ x}\,,\
\end{equation}
find the values of $x$
Problem 247 [Not Unipodal: Complex Numbers]:
This problem is by
Given the relation
\begin{equation}
\frac{\ln z}{z} = \frac{\pi}{2} \,,
\end{equation}
Problem 248 [Unipodal]:
This problem is by
Given the relations
\begin{align}
a^3 + b^3 &= 16\,,\\
a+b &= 4\,,
\end{align}
find the values of $\phi = a^4 + b^4$.
Problem 249 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
5^x\cdot 2^x \cdot x^x = \sqrt{5} \,,
\end{equation}
find the values of $x$
Problem 250 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
e^x+x+1=0 \,,
\end{equation}
find the values of $x$.
Problem 251 [Not Unipodal]:
This problem is by
Given the relation
\begin{equation}
\sqrt{x}=\left( \frac{1}{2}\right)^x \,,
\end{equation}
find the real values of $x$.
My solution here is a little different from that
given by the presenter.

My solution here is a little different from that
given by the presenter.

My solution here is a little different from
that given by the presenter.
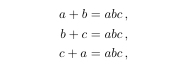
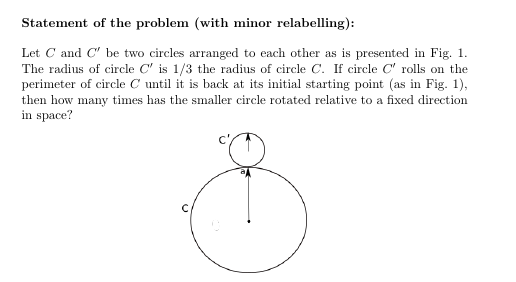
will approach the problem from the standpoint of symmetry. One can find my solution to this
problem at Solution to this problem.
https://www.youtube.com/watch?v=kN3AOMrnEUs
Statement of the problem:
https://www.youtube.com/watch?v=Y-dAhOmR_68
Statement of the problem:
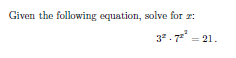
https://www.youtube.com/watch?v=ArVrjYmBhVw
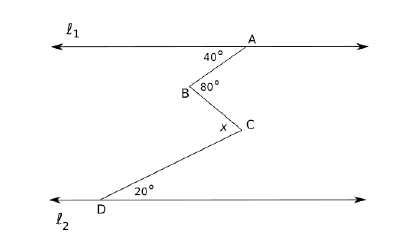
Statement of the problem: Solve for the measure of angle x.
The title of the video is "Google Interview Riddle - 3 Friends Bike
and Walk"
https://www.youtube.com/watch?v=82b0G38J35k
Statement of the problem: Three men will start at point S and transit to point F, using a combination of walking and riding a scooter built for two. Find the minimum time that this can be done in. (Warning: The figure below gives away a lot.)
This problem demonstrates in problem solving the need for clear organization and the creation of helpful visual aids.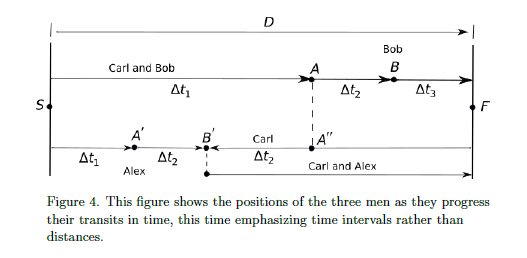
https://www.youtube.com/watch?v=SUMLKweFAYk
The title of the video is ``Steven Strogatz: In and out of love with math | 3b1b podcast #3".
that I
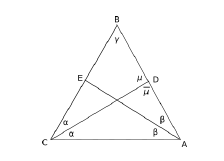
will not take up. It is known as the Steiner-Lehmus Theorem.

https://www.youtube.com/watch?v=zLU5Cagv-Tc
April 17, 2021. My solution here is a little different from that
given by the presenter:
https://www.youtube.com/watch?v=3jnbBVpOf40
Titled: A tricky problem with a 'divine' answer!
April 28, 2024. My solution here is a little different from that
given by the presenter:
https://www.youtube.com/watch?v=k2QONlmEab0
Titled: A very nice olympiad question | How to solve ....
?. Titled: A Nice Algebraic Expansion Problem: My solution
here is a little different from that given by the presenter:
The YouTube video is found at:
https://www.youtube.com/watch?v=-70c48Fl-x4
Titled: Evaluating x sqrt(x)+y sqrt(y)_Math is math
https://www.youtube.com/watch?v=JTt0wjqG7vM
Titled: Harvard University Admission Question ||
Algebra Exam || 99\% Failed Entrance Test
Presenter: Super Academy
https://www.youtube.com/watch?v=vhbLBruwDj0
Titled: A Nice math Olympiad Problem --
You should know this trick
Presenter: Learncommunolizer
https://www.youtube.com/watch?v=C-0anvb3D4k
Titled: Japan | A nice Math Olympiad Algebra Problem
| Find x=? & y=?
Presenter: Super Academy
https://www.youtube.com/watch?v=PaMbwZ1VCTY
Titled: A Mind-blowing Math Olympiad Equation | How to solve!!
Presenter: Master T Maths Class
https://www.youtube.com/watch?v=Iq-ToVDngHA
Titled: A nice Math Olympiad Problem || Find x=? & y=?
Presenter: Super Academy
https://www.youtube.com/watch?v=ubvYMrln5WA
Titled: Algebra | A Nice Radical Problem | Math Olympiad
Problem | How to Solve this | Find X and Y
Presenter: ilm PEDIA
https://www.youtube.com/watch?v=M5jU3a5-brA
Titled: Simplification | Can you Solve This | A Nice Math
Olympiad Algebra Problem | JEE | Find value of X+Y
Presenter: ilm PEDIA
https://www.youtube.com/watch?v=WeOdqkh8tSs
Titled: Harvard University Simplification Tricks | Radical
Algebra Aptitude Test | Ivy League Entrance Exam
Presenter: Super Academy
https://www.youtube.com/watch?v=remIGvjSkV4
Titled:Harvard University Aptitude Test Tricks ||
Algebra Ratio Problem || 1 percent Passed Entrance
|| a+b/a-b=?
Presenter: Super Academy
though I've already encountered many `Olympiad' problems to have a similar form.
Concept of Number},
Birkhauser/Springer, New York, 2013.
`dihedral equation' by Felix Klein.)
https://www.youtube.com/watch?v=mTwpkMCm--w
Titled: Olympiad Mathematics - Algebra Problem |
Vietnamese Junior Math Olympiad
Presenter: Math Booster
https://www.youtube.com/watch?v=tpZRaMFagUg
Titled: Hardest Exam Question | Only 8 percent of
students got this math question correct
Presenter: Higher Mathematics
an `Olympiad'
problem. I changed it subtly.
https://www.youtube.com/shorts/tna_mHHtChw
Titled: Typical SAT Question
Presenter: MrHTutoring
https://www.youtube.com/watch?v=LG0AgRNN1Po
Titled: Cambridge University Exponential Problem ||
Admission Interview tricks
Presenter: Super Academy
https://www.youtube.com/watch?v=a4VP42kz7d0
Titled: Working with Logarithmic Expressions
Presenter: SyberMath
https://www.youtube.com/watch?v=C5HTplGs1AQ
Titled: Evaluating A Nice Polynomial | Math Olympiads
Presenter: SyberMath
https://www.youtube.com/watch?v=LtuCtaW3CYw
Titled:A very tricky math question with factorial
Presenter: Higher Mathematics
https://www.youtube.com/watch?v=Srn-PJwFZgg
Titled: A fun proof for an integer
Presenter: Prime Newtons
https://www.youtube.com/watch?v=_jaPL00JUhU
Titled: Can You Simplify A Radical?
Presenter: SyberMath
https://www.youtube.com/watch?v=GX7MzC0_2oM
Titled: Harvard University Aptitude Test Tricks
|| Algebra Problem
Presenter: Super Academy
https://www.youtube.com/watch?v=aYeuix9nGG0
Titled: Can you pass College Entrance Aptitude Test ?
|| Find x=?
Presenter: Super Academy
https://www.youtube.com/watch?v=zCah09n9Zns
Titled: A very tricky Harvard University Admission
Algebra Exam | Entrance Aptitude Test | Find x=?
Presenter: Super Academy
Presenter: Patrick
https://www.youtube.com/watch?v=9v41Nxu9UMU
Titled: Harvard University Exponential Problem
Presenter: Super Academy
https://www.youtube.com/watch?v=FgUtVjfD4Vw
Titled: A nice Math Olympiad Problem | Algebra Equation
Presenter: Super Academy
https://www.youtube.com/watch?v=4SwFsYsTrms
Titled: Math Olympiad | A Nice Algebra Problem
| Find the values of X
Presenter: Learncommunolizer
https://www.youtube.com/watch?v=JTt0wjqG7vM
Titled:Harvard University Admission Question
|| Algebra Exam
Presenter: Super Academy
https://www.youtube.com/watch?v=RcoaWR0esE0
Titled: Harvard University Aptitude Test Tricks
|| Algebra Problem
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=bIHujxQSmmU
Title: China | Can you solve this ? | Math Olympiad
Presenter: Learncommunolizer
Source: https://www.youtube.com/watch?v=XxbsHOUQjfw
Title: A nice Algebra Problem || Harvard University
Aptitude Test Tricks
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=yEW3O_ToYDE
Title: France | Can you solve this ? | Solution to this problem
Presenter: Learncommunolizer
Source:https://www.youtube.com/watch?v=YEwdgK8COlI
Title:Harvard University Exam Question ||
Algebra Exam
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=8OxLe4BDJbU
Title: Maths Olympiad | How To Solve
Olympiad Maths faster
Presenter: Maths Atoka
Source: https://www.youtube.com/watch?v=LzBdHFx0A8g
Title: Solving Another Quartic Equation | Problem 357
Presenter: aplusbi
Source: ???
Title: ????
Presenter: ????
Source: https://www.youtube.com/watch?v=hBx8RBkRVGg
Title: A Radical Equation With Radicals
Presenter: SyberMath
Source: https://www.youtube.com/watch?v=4FPdSXaydHA
Title: A very tricky Oxford University Exponential Question
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=fkmU5DGp5gM
Title: Stanford University Entrance Interview Tricks
| Find x=?
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=fkmU5DGp5gM
Title: Stanford University Entrance Interview Tricks
| Find x=?
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=Q6vFA8FqKzA
Title: Indian l Olympiad Math Algebric Exponential
| Find x=?
Presenter: Math Master TV
as real, I had no incentive to do so. I would hope that on an actual test,
one would be told what the domain is.]
Source: https://www.youtube.com/watch?v=_Rk0zyqGhO0
Title: Math Olympiad | A Nice Algebra Problem |
A Nice Radical Equation
Presenter: SALogic
https://www.youtube.com/watch?v=XxSzU_YH0gI
Titled: A Nice Algebra maths olympiad problem |
math olympiad questions
Presenter: SouL Institution
Source: https://www.youtube.com/watch?v=jnupmpMDBUI
Title: Stanford University Entrance Aptitude Test
Advanced tricks
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=VVM6SxLnRf0
Title: Harvard University Aptitude Test
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=_-CY3tbAnjA
Titled: Harvard University Entrance Exam tricks
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=wGyFflQj2X00
Title: Advanced Math from Cambridge University
Entrance Exam
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=W4YsEql1QYA
Title: A tricky Algebra Problem from Stanford
University Admission Interview
Presenter: Super Academy
Source: https://www.youtube.com/shorts/I0hQSOopzfs
Title:Challenging Math Olympiad Question
Presenter: Soul Institution
of my using the unipodal algebra to solve these 'olympiad'
problems. I proved a simple but important lemma. Additionally,
I added some unipodal heuristics for consideration.
Source: https://www.youtube.com/watch?v=W0dJwFFGXRw
Title: maths olympiad question || An algebraic
exponential problem
Presenter: Maths Curiosity
Source: https://www.youtube.com/watch?v=ep6a75cg6F8
Title: Germany | Can you solve this ? | Amazing
Olympiad Math Problem
Presenter: Learn Communolizer
Source: https://www.youtube.com/watch?v=rbypW8CQaGQ
Title: A very tricky Question from Oxford
University Entrance Exam
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=lfxCDP7y_D8
Title: A tricky Solution from Stanford University
Admission Interview
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=QnBd2aIVEcQ
Title: A very tricky Question from Stanford
University Entrance Exam
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=xSITkGFst_A
Title: South Africa Math Olympiad Question
Presenter: LKLogic
Source: https://www.youtube.com/watch?v=YoocXFxYMlg
Title: Advanced Math from Harvard University Entrance Exam
Presenter: Asad International Academy
Source: https://www.youtube.com/watch?v=QnBd2aIVEcQ
Title: A very tricky Question from Stanford
University Entrance Exam
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=J87-vA7DTbk
Title: Everything is possible | A tricky math question
Presenter: Higher Mathematics
Presenter: Patrick
to other problems already solved earlier on this page.
Given the relation
\begin{equation}
\left(x - \frac{1}{x}\right)^2 + \left(x +\frac{1}{x}\right)^2 = 2\,,
\end{equation}
find the values of $x$.
Source: https://www.youtube.com/watch?v=NfgEPsm9Jzw
Title: The Hardest Exam Question | Only 6% of
students solved it correctly
Presenter: Higher Mathematics
Source: https://www.youtube.com/watch?v=Aao4AhD9q3A
Title: Mastering The Oxford University Entrance Exam
With These Easy Tricks
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=0IA6Pqs5Rwk
Title: Can You Pass Harvard's Entrance Exam Question ?
Presenter: Asad Internmational Academy
Source: https://www.youtube.com/watch?v=KbELy5Crhf8
Title: Harvard University Admission Exam
|| Logarithms Problem Tricks
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=xGvJkmmQ9XM
Title: Harvard Entrance Exams || No
Calculator Allowed
Presenter: Maths Explorer
Source: https://www.youtube.com/watch?v=lI8DAgFfh9c
Title: Math question for a "true" geniuses
Presenter: Higher Mathematics
Source: https://www.youtube.com/watch?v=cdRpsmKhqx8
Title: Germany - Math Olympiad Problem | Be Careful!
Presenter: Higher Mathematics
Source: ?
Title: ?
Presenter: ?
Source: https://www.youtube.com/watch?v=QZ0LaMSN1EM
Title: STANFORD UNIVERSITY Admission Interview
Secrets Revealed!
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=nuy6sQckL24
Title: A beautiful Question from Harvard University Entrance Exam
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=Ok_rPUyimZc
Title: Math Olympiad - Exponential Trigonometric
Problem - find x!
Presenter: Math Master TV
Source: https://www.youtube.com/watch?v=AJrZvwWpZZU
Title: Spain | A Nice Algebra Problem | Math Olympiad
Presenter: SALogic
Source: https://www.youtube.com/watch?v=3FRNl9Ry8cs
Title: France | A Nice Algebra Problem | Math Olympiad
Presenter: SALogic
Source: https://www.youtube.com/watch?v=mh5UPPaJLXY
Title: Can You Solve This 12-Year-Old’s Math
Problem from China?
Presenter: Global Maths
a double root). I chose a different substitution to experiment
with another technique.
Source: https://www.youtube.com/watch?v=9zkyOc3a2uo
Title: Olympiad Math Question || Nice Algebra Equation
Presenter: Pages by Aapi
Source: https://www.youtube.com/watch?v=X5RhYu88EYI
Title: Mexico | A Nice Algebra Problem
Presenter: SALogic
Source: https://www.youtube.com/watch?v=NWxNdeiQ1Vw
Title: A nice mathematics algebra exponential problem
Presenter: Mathematics and Statistics Guru
Source: https://www.youtube.com/watch?v=Xw8VBHXK81M
Title: Nice Exponential Math Problem |
Harvard Entrance Exam Question
Presenter: SchoolClass Math
Source: https://www.youtube.com/watch?v=Zly87p7fsqY
Title: Harvard University | Can you solve this ?
Presenter: Basic concept of Math
Source: https://www.youtube.com/watch?v=5pa1AryylpM
Title: believe in the math, not wolframalpha
Presenter: Blackpenredpen
Source: ?
Title: ?
Presenter: ?
Source: https://www.youtube.com/watch?v=t6Vzq4DnQH8
Title: A tricky Stanford University Admission Algebra Interview
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=2DdEQWgBlIc
Title: A Nice System Of Logs
Presenter: SyberMath
Source: https://www.youtube.com/watch?v=S64w7YxWoTs
Title: France | Olympic math question - past exam
SAT MATH QUESTION
Presenter: Kmath addict
Source: https://www.youtube.com/watch?v=nL8SN1xaSFc
Title: Cambridge University Admission Exam Tricks
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=5y7JXP7Ow2o
Title: ab= ? | Harvard MIT Math Tournament 2016 | HMMT
Presenter: Math Training
Source: https://www.youtube.com/watch?v=ZlDFHJqUziE
Title: Solving a nice integral - Solution to past exam
Presenter: Kmath addict
Source: https://www.youtube.com/watch?v=nbWqIwTZrSg
Title: Harvad University Admission test
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=yl_0f9wJQeQ
Title: How to solve this nice math rational
Exponential algebra problem
Presenter: Mathematics & Statistics Guru
Source: https://www.youtube.com/watch?v=bcG73tJvGz4
Title: Advance Algebra | Olympiad Mathematics
Presenter: Master T Maths Classes
Source: https://www.youtube.com/watch?v=IGUh3Mv7DAI
Title: One Of The Most Difficult Harvard's
University Entrance Exam
Presenter: Maths with Chinwendu
Source: https://www.youtube.com/watch?v=ZGQcq-BZkOI
Title: Harvard University interview Exam question
Presenter: Maths with Chinwendu
The following problem is an adaptation of a YouTube problem
whose reference I lost.
Source: https://www.youtube.com/watch?v=uofFyT0d1Wc
Title: A Nice Algebra Equations
Presenter: MathMinds
Source: https://www.youtube.com/watch?v=MKsA2YkmVc4
Title: A Very Nice Math Olympiad Problem
Presenter: Spencer's Academy
Source: https://www.youtube.com/watch?v=ZQZMu0SraSQ
Title: Can you Pass Harvard University Admission Interview
Presenter: Enjoy Math
Source: https://www.youtube.com/watch?v=VgIlmBmYKCE
Title: Harvard University Entrance Exam
Presenter: SchoolClass Math
in essentially three different ways.
Source: https://www.youtube.com/watch?v=Ib_sSaAEaUE
Title: Oxford University Entrance Exam Tricks
Presenter: Super Academy
in essentially three different ways.
Source: ?
Title: ?
Presenter: ?
in essentially three different ways.
Source: https://www.youtube.com/watch?v=9MogStH2q3Q
Title: A tricky Algebra from Stanford University
Advanced Aptitude test
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=wuMld8B9d5k
Title: A Nice Math Olympiad Problem
Presenter: Maths Black Board
Source: https://www.youtube.com/watch?v=yGmVy0FZdXY
Title: How to Solve Algebraic Equations
Presenter: Maths Black Board
Source: https://www.youtube.com/watch?v=nv-c8W6keJ0
Title: Portugal | A Nice Algebra Problem | Math Olympiad
Presenter: SALogic
Source: https://www.youtube.com/watch?v=G3KLDzcvKYo
Title: Japanese | Can you solve this ?
Presenter: Learncommunolizer
Source: https://www.youtube.com/watch?v=Ycyag8jY1TQ
Title: So, you want a HARD math question with exponents?
Presenter: Higher Mathematics
Source: https://www.youtube.com/watch?v=ggDoEEcdBp0
Title: Crack This Olympiad Exponential Equation
Presenter: GT Academix
Source: https://www.youtube.com/watch?v=nJwQGTPIyUM
Title: A Nice Math Olympiad Exponential Equation x^x^2 = 16
Presenter: MrMath
Source: ?
Title: ?
Presenter: ?
Source: https://www.youtube.com/watch?v=D-TDK7pQafI
Title: Can you solve this? | Oxford entrance exam question
Presenter: Enjoy Math
Source: https://www.youtube.com/watch?v=Uqk2MS5Lcsk
Title: Math Olympiad | Algebra Problem
Presenter: MathsFocus
Source: https://www.youtube.com/watch?v=VJmVcpfcy3Q
Title: A Tricky Math Olympiad challenge
Presenter: MathsFocus
Source: https://www.youtube.com/shorts/qAxXkDFRvHA
Title: Can you solve this Harvard
Presenter: EngineeringMathShorts
Source: https://www.youtube.com/watch?v=NwbqN7myYhY
Title: Harvard University interview exponential math question
Presenter: JJ Online Maths Class
Source: https://www.youtube.com/watch?v=nXK5scl4DJI
Title: A tricky Entrance Interview Question
from Harvard University
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=oMhDv9tydW0
Title: Can you Solve a tricky Entrance Exam from
Cambridge University ?
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=XXFNxw-2bo8&list
=PLQG1LDIiB85gGzcpH00P_riNifgU_ZOQW&index=22
Title: A Nice Algebra Equation
Cambridge University ?
Presenter: MathMinds
Source: https://www.youtube.com/watch?v=vkdbgkAeVNk&list
=PLQG1LDIiB85gGzcpH00P_riNifgU_ZOQW&index=47
Title: A Nice Math Olympiad Algebra Problem
Presenter: MathMinds
Source: https://www.youtube.com/watch?v=67234_o6z-4
Title: Germany | A nice Logarithmic Math Olympiad Problem
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=MRTDBSwlH2I
Title: Harvard University Admission Exam Tricks
Presenter: Super Academy
Note: This problem is pending final confirmation of results.
Source: https://www.youtube.com/watch?v=nZmxQYLaH2g
Title: Germany | Can you solve this?
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=7zwAqqH6C58&list
=PLMvuVeOn1Hd_KIT-dsvIVluQQN3pJrlmX&index=691
Title: Nice Algebra Math Simplification
Presenter: Master T Maths Class
Source: https://www.youtube.com/shorts/5Rfa6lDU3XY
Title: A Nice Olympiad Algebra Problem
Presenter: Numbers.Numbers
Source: https://www.youtube.com/watch?v=Klef16FHNK4
Title: Japanese | Can you solve this?
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=Gz6VLgvFLHs
Title: A nice Math Olympiad Simplification Problem
Presenter: Super Academy
Source: https://www.youtube.com/shorts/5Rfa6lDU3XY
Title: A Nice Olympiad Algebra Problem
Presenter: Numbers.Numbers
Source: https://www.youtube.com/watch?v=PvE7HiRakQk
Title: A Nice Algebra Problem | Math Olympiad
Presenter: SALogic
Source:https://www.youtube.com/watch?v=7KsIray2pXI&list
=PLMvuVeOn1Hd_KIT-dsvIVluQQN3pJrlmX&index=321
Title: China | Can you solve this ?
Presenter: Masters T Maths Class
Source: https://www.youtube.com/watch?v=7zwAqqH6C58&list
=PLMvuVeOn1Hd_KIT-dsvIVluQQN3pJrlmX&index=691
Title: Nice Algebra Math Simplification
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=CeLKQg9z7LM
Title: Nice Algebra Math Problem
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=lSRh6UJdrlo
Title: Germany | Can you solve?
Presenter: Masters T Maths Class
Source: https://www.youtube.com/watch?v=X5iYlxCwGRo&list
=PLMvuVeOn1Hd_KIT-dsvIVluQQN3pJrlmX&index=46
Title: A Nice Exponential Equation
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=9ljcSSCP8oE
Title: A Nice Algebra Problem | Math Olympiad
Presenter: SALogic
Source: https://www.youtube.com/watch?v=VayJZrGnbLI
Title: Russisa | A Nice Algebra Problem
Presenter: SALogic
Source: https://www.youtube.com/watch?v=dSwi5VSxMWI
Title: A Nice Olympiad Algebra Problem
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=06tHCsynl8w
Title: Nice Square Root Simplification
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=7P4eF0fV3gI
Title: Can You Crack This Radical Equation?
Presenter: InfyGyan
Source: https://www.youtube.com/watch?v=cCPdn0gaIVA
Title: China | Can you solve this?
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=UwHSgLhjiHE
Title: Germany | Can you solve this? ?
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=U5Svh3S7Ziw
Title: A Nice Math Olympiad Algebra Problem
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=3a0EF9j1jIk
Title: A Homemade Equation | Problem 292
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=3a0EF9j1jIk
Title: I Couldn't Solve This Equation - WA did! | 428
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=nBu-7ughFE8&list
=PLMvuVeOn1Hd_KIT-dsvIVluQQN3pJrlmX&index=158
Title:Unlocking the Secrets of a Mind-Bending Math
Olympiad Trigonometric Challenge!
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=nBu-7ughFE8&list
=PLMvuVeOn1Hd_KIT-dsvIVluQQN3pJrlmX&index=158
Title:Unlocking the Secrets of a Mind-Bending Math
Olympiad Trigonometric Challenge!
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=V1ye2oXNp-Y
Title: Russian | Can you solve this ?
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=iEWZXZ8XLew
Title: A Sum of Powers | Problem 421
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=9ljcSSCP8oE
Title: A Nice Algebra Problem | Math Olympiad
Presenter: SALogic
Source: https://www.youtube.com/watch?v=nbWqIwTZrSg
Title: Harvad University Admission test
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=fSfl-Ch1ujI
Title: Japanese | Can you solve this?
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=MjmCfjALFdw
Title: Germany | Can you solve this ?
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=A1shWBxiVns
Title: A Tangential Equation | Problem 361
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=x-IHueYbzuQ
Title: Believe in triangles, not squaring both sides!
Presenter: blackpenredpen
Source: https://www.youtube.com/watch?v=MAvbLgfzcww
Title: Nice Exponent Math Simplification
Presenter: Master T Maths Class
Source: ?
Title: ?
Presenter: ?
Source: https://www.youtube.com/watch?v=uguB0e_8ygs
Title: A Natural Log Problem With Complex Numbers
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=07Elc3M7Tk4
Title: A Proportional Problem of Ratios | Problem 294
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=JxCDIBqtf18
Title: Solving A Viewer Suggested Problem | Problem 238
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=bmsMH_N7l_M
Title: Japanese | Can you solve this?
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=GnE_6JtOpio
Title: A Quatrodecic Equation | Problem 290
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=WhS4BuIqlSc
Title: A Locus Problem | Problem 191
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=mPauY95OQLI
Title: Let's Solve A Problem With Complex Exponentiation
| Problem 164
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=ca_BOHCmRbo
Title: An Imaginarily Exponential Equation
| Problem 386
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=K0k4hdiiDBM
Title: A Ratio of Two Complex Numbers |
Problem 394
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=FhpAdhRMyk0
Title: A Nice Problem from A Nice Book |
Problem 377
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=OMEu36Pth_8
Title: An Exponential Equation and A Special Function |
Problem 200
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=cugNGIoe86o
Title: Interesting radical equation
Presenter: Chidex Online Math Class
Source: https://www.youtube.com/watch?v=BecmY7Gw85g
Title: A Problem With z And Its Conjugate |
Problem 218
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=psS7fG_kFd8
Title: An Imaginary Exponential Equation
Problem 346
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=v9Nsp67iNaM
Title: Harvard University Software Engineering Admission Exam
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=FXEFFSDwglE
Title: A Very Exponential Power Tower
| Problem 272
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=Pj7ju4ebtY0
Title: Can We Solve A Transcendental Equation
Presenter: SyberMath
Source: https://www.youtube.com/watch?v=fE3i7kWdVYA
Title: A Short Locus Problem With Absolute Values
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=G66wNWWpjDM
Title: An Infinite Complex Fraction
Presenter: aplusbi
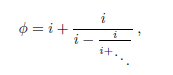
Source: https://www.youtube.com/watch?v=elkUO6eRMvM
Title: Solving 8 Equations w/ Lambert W function
Presenter: blackpenredpen
Source: https://www.youtube.com/watch?v=_lJ1NsXB-gE
Title: Can you Solve Admission Question from
Cambridge University?
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=NQVQyttRC7o
Title: Cambridge University Entrance Exam
Secrets EXPOSED
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=1zLfC_TVP1Y
Title: China | A nice Math Olympiad Exponential Simplification
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=evGZ4AXFILE
Title: High School Mathematics Tournament | Diophantine Equation
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=rqDnyMZ9oiU
Title: Can You Solve? | America's Hard Maths Word Problem
Presenter: Daily Mathematics
A man invested a sum of \$280, partly at
5% and partly at 4%. If the total
interest is \$12.90 per annum,
find the amount invested at 5%.
Source: https://www.youtube.com/watch?v=yl_0f9wJQeQ
Title: How to solve this nice math rational
Exponential algebra problem
Presenter: Mathematics and Statistics Guru
Source: https://www.youtube.com/watch?v=RughThc09xU
Title: Solving A Nice Problem With z-bar
| Problem 139
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=H2GbSHIkybo
Title:Solving An Absolute Value Equation
| Problem 127
Presenter: aplusbi
Source: ?
Title: ?
Presenter: ?
Source: https://www.youtube.com/watch?v=MxdUD2riv4Q
Title: Cambridge University Admission Interview
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=LXCNrSiapMw
Title: I solved A System With Conjugates
| Problem 45
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=suqfQuCzvd0
Title: I Checked A Complex Sum
| Problem 57
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=OBtLU4KcNnk
Title: Finding The Square Root of 2+i
Problem 445
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=sYL9gc5kvIk
Title: A Nice Algebra Equation |
Math Olympiad Questions
Presenter: Maths Black Board
Source: https://www.youtube.com/watch?v=CrQrFA5OWR4
Title: A Homemade Exponential Equation
| Problem 400
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=PXSVw-5GOnQ
Title: How I Solved An Equation With Absolute Value
| Problem 72
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=MUpAYTkP_Zg
Title: I Solved An Equation with z and z bar
| Problem 77
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=yq7FhX0QOtI
Title: Can You Solve An Equation With z(bar) And Modulus?
| Problem 91
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=kxP7mnHNaXY
Title: Cambridge University Admission Exam tricks
Presenter: Super Academy
Source: ?
Title: ?
Presenter: ?
Source: https://www.youtube.com/watch?v=kZY3T8fhF1k
Title: Japanese l can you solve??
Presenter: Math Master TV
Source: https://www.youtube.com/watch?v=Bn5KBONOxDE
Title: I Solved A Complex Cubic System |
Problem 89
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=Q22yx5LUwwU
Title: A Curious Trigonometric Equation
| Problem 307
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=QVB8nZRr2Ao
Title: A Nice Exponential System With Logs
Presenter: SyberMath Short5s
Source: https://www.youtube.com/watch?v=Q_ZGhFwT1w0
Title: You Probably Haven't Seen This Equation Before |
Problem 155
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=dDPelu7GCLs
Title: Exponential Equation Mathematics Problem
Presenter: New Track Mathematics
Source: https://www.youtube.com/watch?v=m_S9Yxx9x-4
Title: A Real Problem with Re(z) |
Problem 181
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=3gYWZlYSlwE
Title: Germany - Math Olympiad Exponential Problem.
Presenter: KK Logic
Source: https://www.youtube.com/watch?v=MImKHu2qPOk
Title: Simplifying An Interesting Sum
Problem 305
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=8QvkcJvrNDI
Title: A Beautiful Homemade Equation
Problem 350
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=qNEpmW3zyis
Title: How to solve this nice math Exponential
algebra problem
Presenter: Mathematics & Statistics Guru
Source: https://www.youtube.com/watch?v=FLLTAHlEqLk
Title: France | Junior Math Olympiad Exponent
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=8WqRzO5XjjM
Title: Harvard University Admission Interview tricks
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=Q_ZGhFwT1w0
Title: You Probably Haven't Seen This Equation Before
Problem 155
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=KQXeTW9G1xg
Title: How To Solve z^4 = z^*
Problem 101
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=E0Z1hism9zU
Title: Let's Solve An Absolute Value Equation
Problem 113 (almost)
Presenter: aplusbi
However, since WolframAlpha agreed with my solution, I decided to
display the modified problem I solved.
Source: https://www.youtube.com/watch?v=et3fY76oy5Q
Title: Solving A Very Exponential Equation
Presenter: SyberMath Shorts
Source: https://www.youtube.com/watch?v=zscAAY-2hII
Title: A Nice Radical Equation With Parameters
Presenter: SyberMath Shorts
Source: https://www.youtube.com/watch?v=ls8t1LAGcBI
Title: Germany Math Olympiad Question
Presenter: Higher Mathematics
Source: https://www.youtube.com/watch?v=dGLjIPkV9GY
Title: An Interesting Nonstandard Equation
Presenter: Syber Math
Source: https://www.youtube.com/watch?v=77Rf1Q0vsAc
Title: Harvard University Admission Interview Tricks
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=LESu08vVvrQ
Title: International Mathematical Olympiad Problem
Presenter: Higher Mathematics
Source: https://www.youtube.com/watch?v=bqFf5R2oofE
Title:How to solve this nice math Exponential algebra problem
Presenter: Mathematics & Statistics Guru
Source: https://www.youtube.com/watch?v=6A5T1uhIozs
Title: An Interesting Homemade Equation
Problem 459
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=XgUcfL7Vj9g
Title: A Nice Absolute Value Equation
Problem 431
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=Xmquv6CpTco
Title: Can We Solve A Tangential Equation
Problem 435
Presenter: aplusbi
Source: https://www.youtube.com/watch?v=wZSxh_WB_JY
Title: An Interesting Nonstandard Equation
Presenter: SyberMath
Source: https://www.youtube.com/watch?v=EMu-kYY5rdE
Title: Is e^x=ln(x) solvable?
Presenter: blackpenredpen
Source: https://www.youtube.com/watch?v=nWWocG37KzI
Title: Oxford University Pure Mathematics Admission Exam
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=zqo4lTXwt5Y
Title: A awesome mathematics problem
Presenter: Mathematics & Statistics Guru
Source: https://www.youtube.com/watch?v=uEYkDU3HoDU
Title: Cambridge University Admission Interview Tricks
Presenter: Super Academy
Source: https://www.youtube.com/watch?v=bCG6L0h5R4A
Title: The Hardest SAT Problem
Presenter: Higher Mathematics
Source: https://www.youtube.com/watch?v=8n1J4goP6vM
Title: A Nice Equation | Problem 433
Presenter: aplusbi
Source: ?
Title: ?
Presenter: ?
Source: https://www.youtube.com/watch?v=QkiWK7mk3bc
Title: Nice Exponent Math Simplification
Presenter: Master T Maths Class
Source: https://www.youtube.com/watch?v=Pj7ju4ebtY0
Title: Can We Solve A Transcendental Equation
Presenter: SyberMath
Source: https://www.youtube.com/watch?v=YknH4GYKdBo
Title: An Interesting Nonstandard Equation
Presenter: SyberMath